--->
22 задач
<---
Источники
#2970
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Муниципальный этап,
Московская область,
Очный этап,
2010,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Андрей Сергеевич — учитель математики в начальной школе. Вчера на уроке он записал на доске выражение вида
a1 ? a2 ? ... ? aN - 1 ? aN = S
и попросил детей заменить вопросительные знаки на знаки сложения и умножения так, чтобы получилось верное равенство. Разумеется, дети быстро справились с заданием. Особенно понравилось Андрею Сергеевичу то, что мальчик Петя нашел сразу два варианта расстановки знаков. Тогда он попросил класс посчитать, сколько всего существует вариантов правильной расстановки знаков. Напишите программу, которая решает данную задачу.
Входные данные
В первой строке содержится число N (1 ≤ N ≤ 30) — количество чисел в левой части равенства, записанного на доске и число S, записанное в правой части равенства (1 ≤ S ≤ 106). В следующей строке даны N целых чисел в том порядке, в каком они были выписаны на доске. Все числа неотрицательные и не превышают 106.
Выходные данные
Выведете на экран одно число –— количество различных вариантов расстановки знаков между числами, приводящих к правильному результату в записанном на доске выражении.
Примеры
Входные данные
2 4 2 2
Выходные данные
2
Входные данные
2 46 4 6
Выходные данные
0
Входные данные
4 8 2 2 2 2
Выходные данные
5
#2982
Темы:
[Обход в ширину]
[Перебор с отсечением]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
2390 год. В заброшенном метрополитене города N-ска завелась громадная змея-мутант. Она ползает вдоль перегонов между станциями, повергая в ужас случайно забредающих под землю потомков людей. Размеры змеи настолько велики, что иногда голова появляется на той станции, вдоль которой еще ползет какая-то другая часть тела, и змея повергает в ужас сама себя. Чтобы избавиться от этой проблемы, змея поймала вас и потребовала написать для нее программу, которая может ей прокладывать кратчайший маршрут для головы от одной станции до другой, не проползая при этом по станциям, где находятся участки ее тела.
Будем называть маршрутом последовательность станций, каждые две последовательные из которых соединены перегоном.
Все перегоны в метрополитене имеют одинаковую длину, а змея имеет длину в \((l - 0.5)\) перегонов. Змея может ползти вдоль перегонов, переползая с одного на другой на станциях. Змея может ползти вдоль перегона только в один слой, а ее голова не может появляться на станции, если в этот момент по станции проползает другая часть ее тела. Змея умеет ползать только головой вперед.
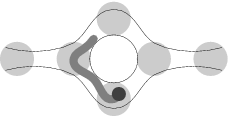
С точки зрения теории графов метрополитен города N-ска является вершинным кактусом. Это означает, что ни одна станция не лежит на двух различных циклических маршрутах и никакие два перегона не соединяют одну и ту же пару станций, никакой перегон не соединяет станцию саму с собой, от каждой станции до любой другой до появления змеи можно было добраться по перегонам.
По заданным карте метрополитена, начальному положению змеи и станции, на которую змея хочет поместить свою голову, выясните, какое минимальное количество перегонов придется проползти змее.
Входные данные
В первой строке ввода записано два числа \(n\) и \(k\) — количество станций и количество перегонов в метрополитене (\(1 \le n, k \le 100\,000\)). В следующих \(k\) строках записано по два различных целых числа \(a\) и \(b\) — номера станций, соединенных соответствующим перегоном.
В следующей строке записано единственное число \(l\), характеризующее длину змеи. В следующей строке записано \(l + 1\) число: номера станций, на которых лежат последовательные части змеи, начиная с головы, а также номер станции, в перегоне к которой лежит хвост змеи длиной в \(0.5\) перегона. Исходно змея расположена таким образом, что ни в каком перегоне не находится одновременно две различных части змеи и змея не пересекает себя ни на какой станции.
В последней строке записано единственное целое число — станция, на которую змея хочет поместить свою голову.
Выходные данные
Если змея сможет выполнить свою задачу, выведите длину пути — количество перегонов, через которые необходимо проследовать голове змеи.
Если задача невыполнима, выведите единственное число \(-1\).
#3143
Темы:
[Задача о рюкзаке]
[Перебор с отсечением]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
Московская областная олимпиада,
2008,
Задача E
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Впервые в жизни Петя летит на международную олимпиаду по программированию. Петя так волновался, что взял с собой множество вещей и теперь во время регистрации на рейс его чемодан не принимают, так как у него превышение разрешенной массы багажа.
У Пети в чемодане лежат N предметов, каждый предмет имеет свой вес Wi килограмм и ценность Ai рублей, причем оказалось так, что для любого предмета выполняется следующее неравенство:
W1 + W2 + … + Wi-1 ≤ Wi
Пете сообщили, что у него перевес чемодана в M килограмм, поэтому ему придется оставить в аэропорту какие-то предметы с суммарной массой не меньше M. При этом Петя хочет понести минимальный урон, а поэтому оставленные предметы должны иметь наименьшую возможную стоимость.
Требуется написать программу, которая подсчитает минимальную возможную стоимость оставленных предметов.
Входные данные
В первой строке задаётся количество предметов в багаже у Пети N (1 ≤ N ≤ 50) и какой у Пети перевес чемодана в килограммах M (1 ≤ M ≤ 1018). Во второй строке задаются N целых неотрицательных чисел – вес всех вещей Wi, сумма чисел не превышает 1018. В третьей строке заданы N целых неотрицательных чисел – ценность всех вещей Ai , все числа не превышают 109.
Выходные данные
В выходной файл требуется вывести минимальную суммарную стоимость предметов, которые Петя будет вынужден оставить в аэропорту.
Ввод | Вывод |
|
|
|
|
#3208
Темы:
[НОД и алгоритм Евклида]
[Перебор с отсечением]
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Региональный этап,
2011,
2 день,
Задача C
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Натуральное число \(a\) называется делителем натурального числа \(b\), если \(b = ac\) для некоторого натурального числа \(c\). Например, делителями числа 6 являются числа 1, 2, 3 и 6. Два числа называются взаимно простыми, если у них нет общих делителей кроме 1. Например, 16 и 27 взаимно просты, а 18 и 24 — нет.
Будем называть нормальным набор из \(k\) чисел (\(a_1, a_2, \ldots, a_k\)), если выполнены следующие условия:
- каждое из чисел \(a_i\) является делителем числа \(n\);
- выполняется неравенство \(a_1 \lt a_2 \lt \ldots \lt a_k\);
- числа \(a_i\) и \(a_{i+1}\) для всех \(i\) от \(1\) до \(k - 1\) являются взаимно простыми;
- произведение \(a_1a_2\ldots a_k\) не превышает \(n\).
Например, набор (2, 9, 10) является нормальным набором из 3 делителей числа 360.
Требуется написать программу, которая по заданным значениям \(n\) и \(k\) определяет количество нормальных наборов из \(k\) делителей числа \(n\).
Входные данные
Первая строка входного файла содержит два целых числа: \(n\) и \(k\) (\(2 \le n \le 10^8\), \(2 \le k \le 10\)).
Выходные данные
В выходном файле должно содержаться одно число — количество нормальных наборов из \(k\) делителей числа \(n\).
Примечание
Правильные решения для тестов, в которых \(n \le 1000\) и \(k = 2\), оцениваются из 30 баллов.
Правильные решения для тестов, в которых \(k = 2\), оцениваются из 60 баллов (в эти баллы включаются также 30 баллов для случая \(n \le 1000\), \(k = 2\)).
Примеры
Входные данные
90 3
Выходные данные
16
Входные данные
10 2
Выходные данные
4
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
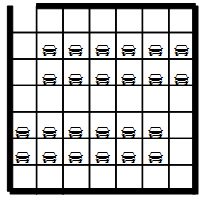
Автостоянка в Цветочном городе представляет собой прямоугольник \(N\times M\) клеток, в каждую из которых можно поставить машину. Стоянка обнесена забором, одна из сторон угловой клетки удалена (это ворота). Машина ездит по дорожке шириной в одну клетку. Незнайку попросили разместить как можно больше машин на стоянке таким образом, чтобы любая машина могла выехать, когда все прочие стоят. Например, на рисунке справа показано, как можно расположить 24 машины на стоянке размером \(7\times 7\). Помогите Незнайке решить эту задачу.
Входные данные
Во входном файле записано два натуральных числа N и M, не превосходящие 7.
Выходные данные
Выведите в выходной файл единственное число: максимальное количество машинок, которое можно расставить на стоянке данного размера.
Примеры
Входные данные
1 3
Выходные данные
1
Входные данные
2 2
Выходные данные
2
Выбрано
:
|