В супермаркете «На троечку» часто происходят распродажи товаров, срок годности которых подходит к концу. Каждый товар привозят в магазин в определенное время, а через некоторое его вывозят из магазина, в связи с окончанием срока годности. Более формально, каждый товар имеет стоимость c _i , время его завоза в магазин a _i и время его вывоза из магазина b _i .

У Иннокентия есть хитрый план похода в магазин. Даже несколько. Каждый план похода в магазин выглядит так: Иннокентий выбирает какое-то время, когда он появится в магазине m _j , время s _j , которое он проведет в магазине среди огромных стеллажей товаров, и сумму денег k _j , которую он рассчитывает потратить. Для каждого плана он хочет узнать, сможет ли он осуществить его, т. е. верно ли, что он сможет во время своего пребывания в магазине купить несколько товаров суммарной стоимостью ровно k _j , при этом все выбранные товары должны быть в магазине на протяжении всего пребывания Иннокентия в магазине.

Помогите Иннокентию определить, какие из его планов можно выполнить.

Вася не только играет в компьютерные и настольные игры, но и решает олимпиадные задачи по программированию. Три года назад он зарегистрировался на одном очень популярном сайте—KodeForces (KF) и с тех пор уже сдал целых 11 задач из архива! Вася не намерен останавливаться на достигнутом и планирует решить еще 1-2 задачи в ближайший месяц - полтора.

Однако сейчас его мозг занят совсем другой проблемой. Раз в год на KF случается чудо — любой пользователь сайта может изменить свой логин (имя пользователя). «Такую возможность упускать нельзя!», — подумал Вася и решил сделать свой логин лаконичным , т.е. состоящим из одинаковых букв.

Однако в этом году все не так то просто... Изменять логин можно только согласно следующему правилу: можно выбрать все одинаковые буквы имени и заменить их все на предыдущую или последующую букву в алфавитном порядке. Например, можно заменить все e на d или f . При этом, z можно заменить на a или y , а a на z или b .

Вася несколько ленив, поэтому, прежде чем начать изменение имени, он хочет посчитать минимальное количество применений описанного выше правила, позволяющее сделать логин лаконичным. Что если это число окажется слишком большим, и он потратит слишком много времени и пропустит очередной рейд в WoW-ке?

Петар организует вечеринку по случаю своего дня рождения и планирует пригласить некоторых сотрудников из компании, где он работает генеральным директором. Каждый сотрудник, включая Петара, имеет уникальный номер от 1 до N и тип шуток, которые он рассказывает, V _i . Также, каждый сотрудник в компании кроме Петара имеет ровно одного начальника. Так как Петар - генеральный директор компании, он имеет номер 1 и руководит всеми сотрудниками (не обязательно напрямую).

На вечеринке есть некоторые правила, которым должны отвечать все присутствующие: 1. На вечеринке не должно быть двух людей с одинаковым типом шуток. 2. Человек не может быть приглашен на вечеринку, если на нее не приглашен его прямой начальник. 3. Человек не может быть приглашен на вечеринку, если типы шуток, которые рассказывает он и его приглашенные подчиненные, не образуют последовательное множество.

Петар хочет знать, сколько возможных наборов типов шуток может быть на его вечеринке, если он пригласит людей в соответствии с вышеуказанными правилами.

Последовательное множество - такое множество, в котором, если отсортировать его по возрастанию, разность между соседними элементами будет равна 1. Например (3, 1, 2) и (5, 1, 2, 4, 3) - последовательные множества, а (2, 5, 3) - нет.

Мирко большой любитель шахмат и программирования, но обычные шахматы уже наскучили ему, поэтому он начал экспериментировать и придумал свою игру. Он взял шахматную доску с N рядами и N столбцами и расположил на ней K ладей. Игра Мирко следует таким правилам: 1. У каждой ладьи есть своя сила, заданная натуральным числом. 2. Ладья видит все клетки поля в своем ряду и своем столбце кроме той, на которой стоит сама. 3. Клетка считается атакованной в том случае, если побитовый XOR сил всех ладей, которые видят эту клетку, положителен. Изначально Мирко некоторым образом расположил ладьи на поле, и теперь собирается сделать P перемещений. Каждый раз он будет брать одну ладью и ставить ее на другую клетку поля (при этом ладья не обязательно будет перемещена вдоль ряда или столбца в котором она стоит). После каждого перемещения, определите сколько клеток на поле атакованы.

Марко обнаружил новую функцию на его телефоне - Т9. На его телефоне имеется стандартная клавиатура на 9 кнопок:

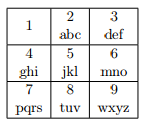
Для того чтобы вводить текст на этой клавиатуре необходимо несколько раз нажимать клавишу с соответствующей буквой. Точнее, если это первая буква на клавише, нужно нажать 1 раз, если вторая буква - 2 раза, и так далее. Например, если мы хотим ввести слово "giht", то необходимо нажать клавиши следующим образом: g-4 i-444 h-44 t-8. Новая возможность, которую открыл Марко, упрощает ввод текста, потому что больше не требуется нажимать по одной клавише несколько раз подряд - достаточно всего одного нажатия. Программа будет пытаться понять, какое слово из словаря вы пытаетесь ввести.

Марко довольно скептически относится к новым технологиями (как минимум к новым для него) и он боится, что ошибки будут довольно часто. Марко наизусть знает весь словарь мобильного телефона. Он состоит из N слов, состоящих из строчных латинских букв, длина каждого слова не превышает 1000000 символов. Марко даст массив нажатий на клавиши S длиной не более 1000, и хочет узнать как много слов из словаря он может получить при такой последовательности нажатий если используется функция Т9.