--->
58 задач
<---
Источники
В факториальной системе счисления основаниями являются последовательность факториалов bk = k!, и каждое натуральное число x представляется в виде:
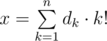, где 0 ≤ dk ≤ k Ваша задача определить по данному в факториальной системе счисления числу его остаток от деления на p.
Входные данные
В первой строке даны два натуральных числа n и p, где n - максимальный индекс такой, что dn ≠ 0 (1 ≤ n ≤ 200, 2 ≤ p ≤ 104). Во второй строке задана последовательность dn, ..., d1, корректно определяющая некоторое натуральное число x.
Выходные данные
Выведите одно число — остаток от деления x на p.
Примеры тестов
Входные данные
5 6
1 3 3 2 1
Выходные данные
5
Примечание
В исходном примере x = 215
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Даны целые числа A0, A1, ..., A5. Найти множество корней уравнения
Входные данные
Дано шесть натуральных чисел A0, A1, ..., A5.
Выходные данные
В единственной строке выведите все корни через пробел. Если корень кратности два, то выведите его два раза (если три, то три и т.д.). Корни выводите в порядке неубывания.
Примеры тестов
Входные данные
120 -226 125 -15 -5 1
Выходные данные
-5 1 2 3 4
Примечание
(x + 5)(x - 1)(x - 2)(x - 3)(x - 4) = x5 - 5x4 - 15x3 + 125x2 - 226x + 120
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Полином
Входные данные
В первой строке даны два целых числа — n и x (1 ≤ n ≤ 1000, |x| ≤ 109). Во второй строке даны n + 1 целое число A0, A1, ..., An — коэффициенты полинома (|Ai| ≤ 109).
Выходные данные
Вывести одно число — значение полинома P(x)
Примеры тестов
Входные данные
2 7
3 2 1
Выходные данные
66
ограничение по времени на тест
6.0 second;
ограничение по памяти на тест
64 megabytes
Полином N-ой степени
Входные данные
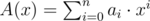
В первой строке даны два натуральных числа n и m (1 ≤ n, m ≤ 40). Во второй строке перечислены коэффициенты a0, a1, ..., an (|ai| < 109).
Выходные данные
Выведите коэффициенты b0, b1, ...bn·m m-ой степени полинома A(x), по одному числу в строке.
Примеры
Входные данные
2 4 1 2 1
Выходные данные
1 8 28 56 70 56 28 8 1
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
64 megabytes
Вычислить коэффициенты A1, A2, ..., An полинома
Входные данные
В первой строке дано натуральное число n (1 ≤ n ≤ 300) Во второй строке перечислены n целых чисел — корни полинома. (|x| ≤ 100)
Выходные данные
Выведите n чисел A0, ..., An - 1 по одному в каждой из n строк — коэффициенты полинома.
Примечание
Полином x2 + 0·x - 1 имеет корни - 1 и 1
Примеры
Входные данные
2 -1 1
Выходные данные
-1 0
Выбрано
:
|