Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.

Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.

Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.

Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.

Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:

1. если вершина красная, то ее родитель – черный;
2. количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.

Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.

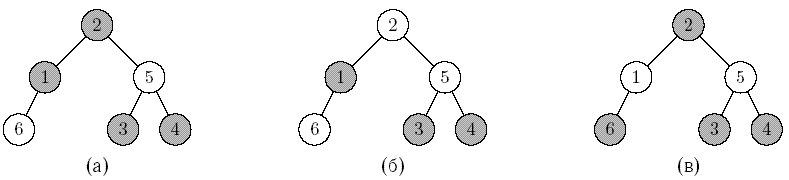Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.

Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.

Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.

Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.

Вася любит искать во всём закономерности. В его тетрадке записаны три числа A,B и C, и он хочет установить между ними какую-нибудь простую закономерность. Для начала он хочет узнать, можно ли этим числам приписать в конец несколько нулей так, чтобы сумма первых двух чисел стала равна третьему. Например, если у него записаны числа 9,34 и 43, то он может не приписывать к ним нулей сумма 9 и 34 и так равна 43. Если же у него записаны числа 23, 7 и 93, то он может приписать нуль к 7 и получить 70. После чего 23 + 70 = 93. Вам дано три натуральных числа A,B и C. Требуется найти неотрицательные целые числа n, m и k, такие что A × 10ⁿ + B × 10^m = C × 10^k.

Петя и Вася играют в очередную интересную игру. У них есть лист бумаги, на котором изображены \(n\) кружочков, помеченных числами от 1 до \(n\). Участники по очереди рисуют стрелочки, соединяющие кружочки. При этом стрелочку из кружочка a в кружочек \(b\) разрешено проводить, если выполнены два условия:

1. еще нет стрелочки из \(a\) в \(b\);

2. нельзя дойти по стрелочкам из \(b\) в \(a\).

Например, в позиции на рис. 1 можно поставить одну из трех стрелочек (рис. 2).

Проигрывает тот, кто не может сделать ход.

Петя решил написать программу, играющую в эту игру. Для этого он хочет сначала посчитать, сколько различных позиций может получиться на доске.