Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Обход в ширину
    0-1 BFS(3 задач)
---> 62 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 7 8 9 10 11 12 13 >> Отображать по:
#3386
Йою Ньерк
  
#3409
Гонки
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На день рождения юному технику Мише подарили машинку с радиоуправлением. Мише быстро наскучило гонять машинку туда-сюда по комнате, и он соорудил специальную трассу. Для этого он разбил комнату на квадратные ячейки, некоторые из них оставив пустыми, а в некоторые поставив препятствия. Целую неделю Миша каждый день улучшал свой рекорд по прохождению трассы. Но каково же было разочарование Миши, когда к нему в гости пришел Тима со своей машинкой и побил его рекорд. Стало понятно, что машинку необходимо модернизировать.

На пробных испытаниях, которые были произведены через день, Миша обнаружил, что машинка действительно ездит лучше, однако ее поведение несколько изменилось. На пульте теперь функционируют только четыре кнопки: вперед, назад, вправо, влево. При нажатии на них машинка едет по направлению к соответствующей стене комнаты, являющейся одновременно границей трассы, точно перпендикулярно ей. Машинка разгоняется до такой скорости, что перестает реагировать на другие команды, врезается в ближайшее препятствие или стену и отскакивает от нее на половину пройденного расстояния, то есть если между машинкой и стеной было x пустых клеток, то после отскока она остановится на клетке, от которой 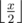клеток до стены (⌊ x⌋ означает округление вниз, например , ).

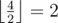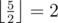Теперь Мише интересно, какое минимальное количество раз необходимо нажать на кнопку пульта, чтобы машинка, начав в клетке старта, остановилась в клетке финиша.

Входные данные

Первая строка входного файла содержит два целых числа n и m — размеры трассы (2 ≤ m, n ≤ 20). Следующие n строк содержат по m символов каждая: символ «.» соответствует пустой клетке, «#» — препятствию, а «S» и «T» — клетке старта и клетке финиша соответственно.

Выходные данные

В выходной файл выведите минимальное количество нажатий на кнопки пульта для проведения машинки по трассе от старта до финиша.

Если доехать от старта до финиша невозможно, выведите  - 1.

Примеры
Входные данные
5 5
S#..T
.#.##
.....
.##.#
.#...
Выходные данные
6
#3489
Поиск в ширину--1
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Напишите программу, которая будет реализовывать поиск в ширину в ориентированном невзвешенном не-мульти графе без петель. Вершины графа являются целыми неотрицательными числами в диапазоне от 0 до N–1 (где N — количество вершин в графе). Граф обязательно представлять списками смежности, а именно — как vector<int>[].

Входные данные

В первой строке задано число NUM — количество различных поисков в ширину, которые нужно выполнить (на разных графах). Далее следуют NUM блоков, каждый из которых имеет следующую структуру.

Первая строка блока содержит два числа N и M, разделенные пробелом — количество вершин и количество ребер графа. Далее следуют M строк, каждая из которых содержит по два числа (разделенные пробелом, от 0 до N–1 каждое) — начало и конец соответствующей дуги. Далее, в последней строке блока, записано единственное число от 0 до N–1 — вершина, начиная с которой нужно запустить поиск.

Количество различных графов в одном тесте NUM не превышает 5, количество вершин N не превышает 60000, количество рёбер M не превышает 125000.

Выходные данные

Выведите на стандартный выход (экран) NUM строк, в каждой из которых по Ni чисел, разделенных пробелами — расстояния от указанной начальной вершины орграфа до его 0-й, 1-й, 2-й и т. д. вершин (допускается лишний пробел после последнего числа). Если некоторая вершина недостижима из указанной начальной, вместо расстояния выводите число 987654321.

Примеры
Входные данные
2
3 2
0 1
1 2
1
4 4
0 1
0 3
1 2
2 3
0
Выходные данные
987654321 0 1 
0 1 2 1
#3491
Поиск в ширину--2 (вершины идентифицируются названиями)
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Напишите программу, которая будет реализовывать поиск в ширину в простом графе, вершины которого не нумерованы и идентифицируются словесными названиями.

Входные данные

В первой строке входных данных задано число NUM — количество различных поисков в ширину, которые нужно выполнить (на разных графах). Далее следуют NUM блоков, каждый из которых имеет следующую структуру.

Первая строка блока содержит целое число M — количество ребер графа. Далее следуют M строк, каждая из которых содержит по два названия — концы соответствующего ребра. Названия гарантированно не содержат пробелов и отделены друг от друга одним пробелом. Далее, в последней строке блока, записано единственное название — вершина, начиная с которой нужно запустить поиск (это название гарантированно хоть раз упоминалась как конец одного из ребер).

Количество различных графов в одном тесте NUM не превышает 5, количество рёбер в графе не превышает 50000.

Выходные данные

Выведите на стандартный выход (экран) NUM блоков, в каждом из которых записаны расстояния от указанной начальной вершины до всех достижимых (если есть недостижимые вершины, они вообще не упоминаются). Перечень должен быть отсортирован по названиям вершин, каждая пара (название, расстояние) должна выводиться в отдельной строке, блоки должны быть отделены друг от друга строкой «===» (три знака «равно»).

Примечание

Задачу можно решить, пользуясь map<string,int> и vector<string> для преобразований имен в номера и номеров в имена; тогда внутри программы можно использовать представление графа как vector<vector<int> >. Для вывода в отсортированном порядке использовать прохождение по всем элементам от begin() до end() структуры map<string,int> (превращающей названия в номера).

Другой способ — вообще отказаться от нумерации вершин числами и представлять граф как map<string,vector<string> >; в этом случае массивы, используемые самим поиском, следует заменить на map<string,int>.

Примеры
Входные данные
2
2
Cherk Zol
Cherk Sm
Zol
4
A Bb
Bb Ccc
Ccc A
Dddd Eeeee
Bb
Выходные данные
Cherk 1
Sm 2
Zol 0
===
A 1
Bb 0
Ccc 1
#3861
8B: кони ходят по очереди
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Переведите каждого из двух коней из одной клетки в другую за наименьшее общее число ходов. Два коня не могут одновременно находиться в одной клетке. Ходы коней должны чередоваться.

Входные данные

Во входном файле записаны координаты первого и второго коня, затем координаты клеток, куда нужно их переместить.

Выходные данные

Программа должна вывести последовательность ходов коней в виде нескольких строк. Первым символом в строке должен быть номер коня (1 или 2), затем, через пробел, координаты клетки, в которую он переставляется. Необходимо вывести любое из возможных оптимальных решений. Кони должны ходить по очереди, первым может ходить любой из коней, кони могут сделать различное число ходов.

Примеры
Входные данные
a1
c2
c2
a1
Выходные данные
1 b3
2 a1
1 d4
2 b3
1 c2
2 a1
Страница: << 7 8 9 10 11 12 13 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест