Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Обход в ширину
    0-1 BFS(3 задач)
---> 20 задач <---
Источники --> Личные олимпиады
    Олимпиады сайта(17 задач)
    Школьная личная олимпиада ФМШ №2007 г. Москвы(7 задач)
    Золотая середина (Новосибирск)(10 задач)
    Нижегородская олимпиада школьников(42 задач)
    Московская олимпиада школьников(168 задач)
    Индивидуальная олимпиада по информатике и программированию (ИОИП)(22 задач)
    Открытая олимпиада школьников(173 задач)
    Украинские олимпиады(61 задач)
    Республиканская олимпиада школьников (Беларусь)(6 задач)
    Жаутыковские олимпиады(8 задач)
    Всероссийская олимпиада школьников(304 задач)
    Международные олимпиады(32 задач)
    Central European Olympiad in Informatics (4 задач)
    Интернет-олимпиады(2 задач)
    COCI(36 задач)
    Турнир Архимеда(36 задач)
    Baltic Olympiad in Informatics(10 задач)
Страница: 1 2 3 4 >> Отображать по:
#14
Сталкер
  
Темы: [0-1 BFS]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

В городе Н при невыясненных обстоятельствах территория одного из заводов превратилась в аномальную зону. Все подъезды к территории были перекрыты, а сама она получила название промзоны. В промзоне находятся N зданий, некоторые из них соединены дорогами. По любой дороге можно перемещаться в обоих направлениях.

Начинающий сталкер получил задание добраться до склада в промзоне. Он нашел в электронном архиве несколько карт территории промзоны. Так как карты составлялись разными людьми, то на каждой из них есть информация только о некоторых дорогах промзоны. Одна и та же дорога может присутствовать на нескольких картах.

В пути сталкер может загружать из архива на мобильный телефон по одной карте. При загрузке новой карты предыдущая в памяти телефона не сохраняется. Сталкер может перемещаться лишь по дорогам, отмеченным на карте, загруженной на данный момент. Каждая загрузка карты стоит 1 рубль. Для минимизации расходов сталкеру нужно выбрать такой маршрут, чтобы как можно меньшее число раз загружать карты. Сталкер может загружать одну и ту же карту несколько раз, при этом придется заплатить за каждую загрузку. Изначально в памяти мобильного телефона нет никакой карты.

Требуется написать программу, которая вычисляет минимальную сумму расходов, необходимую сталкеру, чтобы добраться от входа в промзону до склада.

Входные данные

В первой строке входных данных содержатся два натуральных числа N и K (2 ≤ N ≤ 2000; 1 ≤ K ≤ 2000) — количество зданий промзоны и количество карт соответственно. Вход в промзону находится в здании с номером 1, а склад — в здании с номером N.

В последующих строках находится информация об имеющихся картах. Первая строка описания i-ой карты содержит число ri — количество дорог, обозначенных на i-ой карте. Затем идут ri строк, содержащие по два натуральных числа a и b (1 ≤ a, b ≤ N; a ≠ b), означающих наличие на i-ой карте дороги, соединяющей здания a и b. Суммарное количество дорог, обозначенных на всех картах, не превышает 300 000 (r1 + r2 + … + rK ≤ 300 000).

Выходные данные

Выведите одно число — минимальную сумму расходов сталкера. В случае, если до склада добраться невозможно, выведите число –1.

Примеры
Входные данные
12 4
4
1 6
2 4
7 9
10 12
3
1 4
7 11
3 6
3
2 5
4 11
8 9
5
3 10
10 7
7 2
12 3
5 12
Выходные данные
3
#608
Витрина
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Зал супермаркета имеет форму прямоугольника размером \(M\) x \(N\), в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.

В супермаркет привезли новую супервитрину размером \(K\) x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.

Входные данные

В первой строке вводятся три натуральных числа \(M\), \(N\) и \(K\) (\(M\), \(N\) ≤ 100, \(K\) ≤ \(M\)). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число \(V\) – количество витрин (0 ≤ \(V\) ≤ \(N\)*\(M\)). В следующих \(V\) строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до \(M\)–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до \(N\)–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.

Выходные данные

В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:

U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать \(N\) x \(M\).

Если возможных маршрутов несколько, то выведите любой из них.

Примеры
Входные данные
10 10 5
0
Выходные данные
0
RUURUURUURUURU
Входные данные
9 3 2
4
2 0
5 1
5 2
8 2
Выходные данные
1
URRRDRRRRUU
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
#1003
Вырезанные фигуры
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
4 megabytes
Дано клетчатое поле и вырезанные на нем полосы (вертикальные или горизонтальные). Необходимо подсчитать, сколько фигур вырезано.

Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.

<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).

Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.

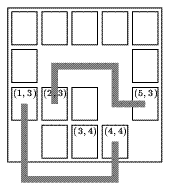
На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:








































































 

Рис 1.

Исходный клеточный лист с вырезанными фигурами

Размер листа: M=6, N=12.

Количество вырезанных фигур: 3

1

1

1

1

1

1

1

1

1

1

1

1

1

0

0

1

1

1

0

0

0

0

0

1

1

0

0

1

1

1

1

0

0

1

1

1

1

1

1

1

1

0

0

0

0

0

1

1

1

1

0

0

1

1

1

0

1

0

1

1

1

1

0

0

1

1

1

1

1

1

1

1
 

Рис 2.

Такая таблица строится в памяти сканера

После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:

Пункт 1. Сколько клеток было вырезано из листа?

Пункт 2. Сколько фигур было вырезано?

Описание формата представления таблицы

Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:

  • направление (0—горизонтальная, 1—вертикальная)
  • (i, j) — координаты начальной клетки полосы (начальной является самая левая клетка для горизонтальной полосы, и самая верхняя — для вертикальной), i — номер строки клетки, j — номер столбца
  • d — длина полосы (количество подряд стоящих единиц).>

Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:

  • В каждой клетке начинается не более одной полосы.
  • Полосы перечислены в порядке следования их начальных клеток (клетки перечисляются по строкам сверху вниз, в строке — слева направо).
  • Общее число полос не превышает 256000.

Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.

Входные данные

Во входном файле записано сначала число \(P\) (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа \(M\) и \(N\) \((1 \le M \le 4000, 1 \le N \le 4000)\). Затем записано число \(K\) \((0 \le K \le 256000)\) — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).

Выходные данные

В выходной файл выведите искомое количество (если \(P=1\), то — количество клеток, вырезанных из листа, если \(P=2\), то — количество фигур, вырезанных из листа).

Примеры
Входные данные
1
40 400
2
1 1 100 40
0 1 101 1
Выходные данные
15959
Входные данные
2
40 400
2
1 1 100 40
1 1 101 1
Выходные данные
2
#1010
Игра с фишками
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
32 megabytes
Задан лабиринт и пары клеток. Требуется определить, существует ли путь между парами.

Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).

Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:

  1. Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
  2. Путь не должен пересекать других фишек.

При этом часть пути может оказаться вне доски. Например:

 

Фишки с координатами (1,3) и (4,4) могут быть соединены. Фишки с координатами (2,3) и (5,3) тоже могут быть соединены. А вот фишки с координатами (2,3) и (3,4) соединить нельзя – любой соединяющий их путь пересекает другие фишки.

Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или «мнимых клеток», расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).

Входные данные

Первая строка входного файла содержит два натуральных числа: W – ширина доски, H – высота доски (1≤W,H≤75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ «X» (заглавная английская буква «экс») обозначает фишку, символ «.» (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырёх натуральных чисел, разделённых пробелами – X1, Y1, X2, Y2, причём 1≤X1,X2≤W, 1≤Y1,Y2≤H. Здесь (X1, Y1) и (X2, Y2) – координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1,1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса; см. далее). Последняя строка содержит запрос, состоящий из четырёх чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.

Выходные данные

Для каждого запроса необходимо вывести одно целое число на отдельной строке – длину кратчайшего пути, или 0, если такого пути не существует.

Примеры
Входные данные
5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
Выходные данные
5
6
0
Входные данные
4 4
XXXX
XXXX
XXXX
XXXX
1 1 2 1
2 2 3 2
1 1 3 1
3 4 4 3
2 1 2 4
1 1 2 2
0 0 0 0
Выходные данные
1
1
4
6
11
0
Страница: 1 2 3 4 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест