Мосты(2 задач)
Применение обхода в глубину(3 задач)
Топологическая сортировка(2 задач)
Точки сочленения(1 задач)
Имеется неориентированный граф, состоящий из \(N\) вершин и \(M\) ребер. Необходимо проверить, является ли граф деревом. Напомним, что дерево — это связный граф, в котором нет циклов (следовательно, между любой парой вершин существует ровно один простой путь). Граф называется связным, если от одной вершины существует путь до любой другой.
Во входном файле в первой строке содержатся два целых числа \(N\) и \(M\) (\(1 \le N \le 100\), \(0 \le M \le 1\,000\)), записанные через пробел. Далее следуют \(M\) различных строк с описаниями ребер, каждая из которых содержит два натуральных числа \(A_i\) и \(B_i\) (\(1 \le A_i < B_i \le N\)), где \(A_i\) и \(B_i\) — номера вершин, соединенных \(i\)-м ребром.
В выходной файл выведите слово «YES», если граф является деревом, или «NO» в противном случае.
3 2 1 2 1 3
YES
Совсем недавно Али-Баба узнал от своего брата Касима об удивительной игре Го. В Го играют на прямоугольной доске – гобане, расчерченном вертикальными и горизонтальными линиями. Все линии пронумерованы. В игре участвуют два игрока, которые по очереди выставляют на гобан камни – специальные круглые фишки. Каждый камень ставится на незанятую точку пересечения линий доски (пересечения называют пунктами). У одного игрока – черные камни, у другого – белые. Камни одного цвета, смежные по вертикали, либо по горизонтали (но не диагонали), объединяются в группу. Одиночный камень также считается группой.
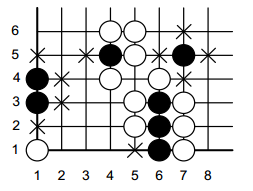
Один из способов набрать очки в Го – захватить камни противника. Каждый камень может иметь от двух до четырех смежных с ним пунктов (по вертикали и горизонтали, но не по диагонали). Если такой пункт не занят камнем, то он называется «дамэ». Дамэ группы – это все дамэ камней, составляющих группу. Как только оппонент своими камнями закрывает все дамэ чужой группы, то эта группа считается захваченной и снимается с доски. Если у группы осталось лишь одно дамэ, то говорят, что эта группа находится в «атари» т.е. на один шаг от захвата соперником.
Дамэ черных камней на рисунке отмечены крестиком. Группа черных из камней (1, 3) и (1, 4) имеет 4 дамэ. Группа (6, 1), (6, 2) и (6, 3) имеет одно дамэ и находится в атари. Черный камень (4, 5) также находится в атари. Помогите Али-Бабе, который всегда играет черными, определить, какие его группы находятся в атари.
Описание каждого теста начинается со строки, содержащей число N – размерность игровой доски (6 ≤ N ≤ 19). Далее следует N строк по N символов каждая. Каждый символ описывает один пункт доски. «B» означает черный камень, «W» – белый, «.» означает пустой пункт. Все группы на доске имеют хотя бы одно дамэ.
Выводите одно число – количество групп черных камней, находящихся в атари.
9 ......... ......... ......... ...WW.... ...BW.B.. B..W.W... B...WBW.. ....WBW.. W....BW..
2
6 WB.WBB .B.W.B ..WW.W WWW..W ..W... BBW...
1
Всем известно, что в позапрошлом веке ковбои занимались перегоном скота. Перегон скота всегда считался опасным делом. Ковбой Джон, готовясь к очередному перегону, изучал план местности. Так как местность гористая, то добраться из одного поселения в другое можно только по дорогам, возможно через другие поселения. Главной опасностью на пути были бандиты, проживающие в разных населенных пунктах, и организующие группировки для нападения на ковбоев. Чтобы их разобщить, Джон разработал гениальный план полной изоляции поселений друг от друга.
Посоветовавшись с напарниками, Джон пришел к выводу, что временно дороги можно вывести из строя, устроив камнепад. Под покровом ночи можно выехать из одного населения в другое, остановиться где-то посреди дороги и устроить камнепад так, чтобы по этой дороге нельзя больше проехать никому. Камни падают позади повозки, поэтому обратной дороги нет. Но зато можно ехать в другой населенный пункт, и если из него существуют дороги, то и их можно вывести из строя.
Сам Джон этого сделать не может, только он знает тайные тропы и должен перегонять стадо. Поэтому он решил использовать наемников. Наемники есть в любом поселении и в любом количестве, однако, за каждого из них приходится платить немалую сумму, поэтому Джон хочет потратить как можно меньше денег. Помогите Джону определить минимальное число наемников, которые смогут привести в непригодность абсолютно все дороги и изолировать все поселения.
В первой строке каждого теста находятся два целых неотрицательных числа N (0 < N < 1000) – количество поселений и M (0 ≤ M ≤ 100 000) – количество дорог, их соединяющих. Далее следует M строк, содержащих описание дорог. В i-й строке находятся два натуральных числа V и U (1 ≤ V, U ≤ N) – номера поселений, которые соединяет i-я дорога. Между двумя различными поселениями существует не более одной дороги, но может существовать несколько маршрутов. Нет дорог, которые образуют петлю, исходящую из поселения и ведущую в него же, не заходя в другие поселения. Не гарантируется, что существует маршрут между любой парой поселений. Маршрутом называется такая последовательность поселений s1-s2- … -sn, что любые два последовательных поселения si и si+1 соединены дорогой..
Выведите минимальное количество наемников, необходимое для изоляции всех поселений.
6 6 1 2 2 3 1 3 4 5 5 6 4 6
2
Вам задан связный ориентированный граф с \(N\) вершинами и \(M\) ребрами (\(1 \leq N \leq 20000\), \(1 \leq M \leq 200000\)). Найдите компоненты сильной связности заданного графа и топологически отсортируйте его конденсацию.
Граф задан во входном файле следующим образом: первая строка содержит числа \(N\) и \(M\). Каждая из следующих \(M\) строк содержит описание ребра – два целых числа из диапазона от 1 до \(N\) – номера начала и конца ребра.
На первой строке выведите число \(K\) – количество компонент сильной связности в заданном графе. На следующей строке выведите \(N\) чисел – для каждой вершины выведите номер компоненты сильной связности, которой принадлежит эта вершина. Компоненты сильной связности должны быть занумерованы таким образом, чтобы для любого ребра номер компоненты сильной связности его начала не превышал номера компоненты сильной связности его конца.
10 14 4 9 7 8 2 5 1 4 9 2 10 6 6 5 8 3 5 9 4 3 8 7 5 1 2 1 6 10
4 3 3 4 3 3 2 1 1 3 2
В Берляндии скоро появятся свои авиалинии. Комитет по разработке берляндских авиалиний уже предложил свой вариант соединения городов авиарейсами. Каждый авиарейс задается парой различных городов. Рейсы односторонние. Президенту понравился план, однако он показался ему чересчур неэкономным. Требуется разработать новый план, который содержит наименьшее количество авиарейсов и удовлетворяет условию: если из города a можно было попасть в город b (возможно, с пересадками) согласно первоначальному плану, то и в новом плане это должно быть возможным. Если же это было сделать невозможно, то и согласно новому плану это не должно быть возможным. Очевидно, что из любого города можно попасть в него самого.
В первой строке входного файла записаны целые числа \(N\) и \(M\) (\(1 \leq N \leq 1000\), \(0 \leq M \leq 10000\)), где \(N\) – количество городов в стране, а \(M\) – количество авиарейсов в первоначальном плане. Города нумеруются от 1 до \(N\). Далее записано \(M\) пар различных чисел \(a_i\), \(b_i\) обозначающих наличие рейса из \(a_i\) в \(b_i\) в первоначальном плане (\(1 \leq a_i \leq N\), \(1 \leq b_i \leq N\)). Пары разделяются пробелами или переводами строк. Между парой городов может быть более одного авиарейса.
В первую строку выходного файла выведите количество рейсов в новом плане. Далее выведите авиарейсы в формате, аналогичном формату входных данных. Пары разделяйте пробелами или переводами строк. Пары выводите в любом порядке. Если существует несколько решений, выведите любое.
Тесты при \(N \le 20\), \(M \le 40\) оцениваются в 40 баллов и только при прохождении всех тестов группы.
Остальные тесты оцениваются независимо, но только при прохождении всех тестов первой группы.
4 5 1 2 2 3 2 1 3 2 2 4
4 1 3 3 2 2 1 2 4