В парке растут два очень высоких дерева, на стволе каждого из которых расположены дупла одно под другим на равном расстоянии друг от друга. Однажды N дятлов решили заселить эти дупла. Некоторые из них знакомы и поэтому хотели бы иметь возможность летать друг к другу в гости. Дятлы летают прямолинейно и очень быстро. Чтобы уменьшить вероятность столкновения, они решили селиться по следующему принципу:
Каждые две дятла, которые хотят летать друг к другу в гости, должны жить на разных деревьях Отрезки, соединяющие дупла знакомых между собой дятлов не пересекаются (однако их концы могут совпадать).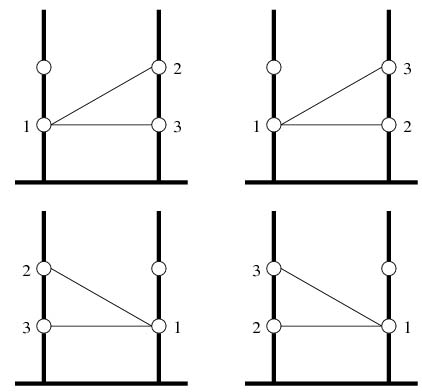
Кроме того, дятлы хотят жить как можно ниже, т.е. на каждом из деревьев они занимают дупла подряд, начина снизу. На каждом из деревьев больше дупел, чем общее количество дятлов.В первой строке содержатся три числа: \(N\) – количество дятлов (\(1 \leq N \leq 10^6\)), \(M\) – количество пар знакомых дятлов (\(1 \leq M \leq 10^7\)) и число \(K\) (\(1 \leq K \leq 2\times 10^6\)). Дятлы занумерованы от \(1\) до \(N\). В следующих \(M\) строках заданы два числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq N\)), задающие пару знакомых дятлов.
Вывод должен содержать одно число: количество вариантов размещения по модулю K.
3 2 10 1 2 1 3
4
4 4 17 1 2 1 3 4 2 3 4
0
Дан неориентированный невзвешенный граф. Необходимо определить, является ли он деревом.
В первой строке входного файла содержится одно натуральное число N (N ≤ 100) -- количество вершин в графе. Далее в N строках по N чисел -- матрица смежности графа: в i-ой строке на j-ом месте стоит 1, если вершины i и j соединены ребром, и 0, если ребра между ними нет. На главной диагонали матрицы стоят нули. Матрица симметрична относительно главной диагонали.
Вывести YES, если граф является деревом, NO иначе.
2 0 1 1 0
YES
5 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0
NO
В селе Максоярославке коровы обычно пасутся на лужайках, соединенных дорожками, на каждой лужайке пасется хотя бы одна корова. При этом для каждой пары лужаек есть ровно один способ пройти от одной лужайки до другой. По каждой дорожке можно двигаться в обоих направлениях. Считается, что все дорожки имеют одинаковую длину.
Главный фермер села хочет построить на лужайках \(k\) коровников для своих коров. Ясно, что каждая корова вечером будет возвращаться именно в тот
коровник, который ближе к ее лужайке (если расстояние до коровников
одинаково, то в любой из них). Поэтому возникает задача определения
такого расположения коровников, при котором наибольшее из расстояний,
проходимых коровами, было бы минимально.
В первой строке входного файла содержатся два числа \(n\) и \(k\) (\(2 \le n \le 50\;000\), \(1 \le k \le n\)) --- количество лужаек и планируемое число коровников, соответственно. Следующие \(n - 1\) строк содержат описания дорожек. Каждая дорожка задается парой целых положительных чисел (\(a, \, b\)), где \(a\) и \(b\) --- номера лужаек, которые соединяет данная дорожка. Лужайки нумеруются с единицы.
В первой строке входного файла выведите \(l\) --- максимальное количество дорожек, по которым придется пройти корове, чтобы попасть в коровник. Во второй строке выведите \(k\) различных целых чисел --- номера лужаек, на которых следует построить коровники. Если оптимальных решений несколько, разрешается вывести любое из них.
7 2 5 4 4 3 1 3 2 3 4 6 6 7
2 1 4
Петя работает в межгалактическом агентстве путешествий. Он часто получает запросы на поиск пути между двумя планетами по доступным межпланетным дорогам. Петя уже сделал по этому поводу целый ряд наблюдений, и сейчас его интересует следующее. Для каждой планеты \(А\) он хочет знать количество пар планет \(В\) и \(С\), таких что любой путь от планеты \(В\) к планете \(С\) проходит через планету \(А\).
Первая строка входного файла содержит два числа \(2 \leq N \leq 20000\) и \(1 \leq M \leq 200000\) – число планет и число дорог соответственно. Далее в \(M\) строках следуют описания дорог. По дорогам можно двигаться в обе стороны. Каждая дорога описывается номерами планет, которые она соединяет. Гарантируется, что от любой планеты можно добраться до любой другой.
В выходной файл выведите \(N\) чисел – для каждой планеты \(А\) выведите количество пар различных планет, таких что любой путь от одной до другой содержит \(А\).
7 9 1 2 1 3 1 4 1 5 1 6 1 7 2 3 4 5 6 7
18 6 6 6 6 6 6