Дан неориентированный невзвешенный граф. Необходимо определить, является ли он деревом.
В первой строке входного файла содержится одно натуральное число \(N\) (\(N\) ≤ 100) - количество вершин в графе. Далее в \(N\) строках по \(N\) чисел - матрица смежности графа: в \(i\)-ой строке на \(j\)-ом месте стоит 1, если вершины \(i\) и \(j\) соединены ребром, и 0, если ребра между ними нет. На главной диагонали матрицы стоят нули. Матрица симметрична относительно главной диагонали.
Вывести "YES", если граф является деревом, и "NO" иначе.
6 0 1 1 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0
NO
3 0 1 0 1 0 1 0 1 0
YES
В городском управлении милиции одного прибрежного города ведется расследование крупного дела, в котором могут быть замешаны сотрудники милиции. Было принято решение о тайной установке оборудования для просмотра информации, поступающей через Интернет. Под подозрение попадают два отдела, но добиться выделения денег на покупку двух комплектов оборудования не удалось. К счастью, внутренняя сеть управления имеет древовидную структуру, то есть каждый отдел имеет выход в Интернет через какой-либо другой отдел. Исключение составляет отдел по борьбе с компьютерными преступлениями, который имеет непосредственный доступ в Интернет по модемной линии.
Можно было бы установить оборудование для слежения прямо в этом отделе, но лучше найти такое расположение, чтобы нарушалась секретность как можно меньшего количества лишних отделов. Решение этой задачи поручили вам.
Подчиненные уже пронумеровали все отделы числами натуральными числами, начиная с 1, первый номер присвоен отделу по борьбе с компьютерными преступлениями.
Первая строка входного файла содержит натуральное число n (n ≤ 30000) — количество отделов. Во второй строке записаны номера отделов, за которыми необходимо установить слежение. На третьей строке находятся n - 1 натуральных чисел, i-е из них не больше i и задает номер отдела, к которому подсоединен отдел i + 1.
В выходной файл выведите одно число — номер отдела, в котором следует установить следящее оборудование.
4 3 4 1 1 3
3
8 3 6 1 1 2 4 5 1 1
1
Мэр города Гадюкино решил проверить состояние дорог после только что проведенного капитального ремонта. Для этого он хочет проехать по каждой дороге в обоих направлениях.
Помогите мэру составить кратчайший маршрут, проходящий по каждой дороге в каждом направлении хотя бы один раз.
В городе Гадюкино n перекрестков и m дорог, каждая из которых соединяет два различных перекрестка. Между двумя перекрестками может быть не более одной дороги.
Известно, что по дорогам от каждого перекрестка можно доехать до любого другого.
Входной файл содержит целые числа n и m (1 ≤ n ≤ 104, 1 ≤ m ≤ 105), и далее m пар целых чисел ai и bi — номера перекрестков, которые соединяет i-я дорога.
Выведите число s — минимальную длину пути и далее s + 1 число — номера перекрестков в том порядке, в котором их нужно проезжать.
3 3 1 2 2 3 1 3
6 1 3 2 1 2 3 1
После тысячелетнего правления большей частью Млечного Пути начался окончательный распад КОсмического ОБъединения ОЛигархов на несколько независимых монархий. КОБОЛ является высокоорганизованной империей, которая имеет форму огромного прямоугольного параллепипида n * m * k парсеков. Империя КОБОЛ сильно засекречена, поэтому лишь немногие знают точные значения n, m и k. Для облегчения контроля империя разделена на nmk маленьких владений по одному кубическому парсеку каждое. Эти владения занумерованы следующим образом:
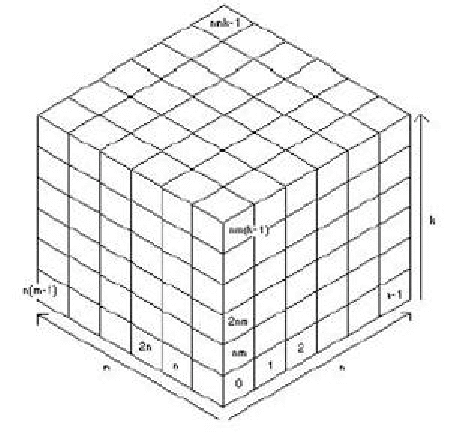
На вход может подаваться сразу несколько тестов. Первая строка содержит положительное целое число - количество тестов. Первая строка каждого отдельного теста содержит четыре целых числа: n m k l, где n, m и k (1 ≤ n, m, k ≤ 30) — размеры империи, а l — количество независимых монархий, на которое должна распасться империя. Далее следуют l строк с описаниями монархий. Каждая из них имеет следующий вид: p d1 d2 ... dp , где p — количество владений, входящих в монархию (1 ≤ p ≤ 20), а d1, ..., dp — номера этих владений. Монархии перечислены в порядке их отделения от империи.
Для каждого теста вы должны на отдельной строке выдать одно целое число — количество месяцев, в течение которых империя будет не связна.
2 2 2 3 9 2 4 5 3 6 8 10 1 7 1 2 1 11 1 9 1 1 1 0 1 3 2 2 3 3 4 0 1 2 3 4 4 5 6 7 4 8 9 10 11
4 0
До наступления летнего сезона ремонта теплотрасс по улицам города можно было проехать от любой площади до любой другой. При ремонте теплотрассы под какой-либо площадью движение по ней полностью перекрывается. Требуется определить, под какими из площадей ремонт теплотрассы нарушает возможность проезда из любого конца города, не затронутого ремонтом, в любой другой. Учесть, что в один и тот же момент времени ремонтная бригада работает только на одной из площадей.
В первой строке входного файла находятся числа N — количество площадей в городе и М — количество улиц их соединяющих (1 ≤ N ≤ 2000, 1 ≤ M ≤ 200000). Площади имеют номера от 1 до N. В каждой из следующих M строк находится пара натуральных чисел, описывающая между какими двумя площадями проходит соответствующая улица (две площади соединяются не более чем одной улицей).
На первой строке выведите число C — количество площадей, ремонт на которых недопустим. На следующей строке выведите C целых чисел — номера этих площадей в возрастающем порядке.
5 6 1 2 2 3 1 3 3 4 3 5 4 5
1 3