Мосты(2 задач)
Применение обхода в глубину(3 задач)
Топологическая сортировка(2 задач)
Точки сочленения(1 задач)
После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету
Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.
Панкрату понравилась игрушка, которая находится в узле с номером \(v\).
Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).
В первой строке входного файла задано число \(n\) — количество узлов в лабиринте. В последующих n строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).
Описание k-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k\) < \(a_k\) <= \(n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k\) = \(u_k\) = 0. Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k\) < \(b_k\) <= \(n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k\) = \(w_k\) = 0.
В последней строке задано целое число \(v\) (1 <= \(v\) <= \(n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.
Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка
Выходной файл должен содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число −1.
Данная задача содержит две подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
1 <= \(n\) <= 100
1 <= \(u_k\); \(w_k\) <= 300
Подзадача оценивается в 50 баллов.
1 <= \(n\) <= \(10^5\)
1 <= \(u_k\); \(w_k\) <= \(10^9\)
Подзадача оценивается в 50 баллов.
В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:
Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:
Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:
7 2 1 3 2 0 0 6 3 4 1 5 1 0 0 0 0 7 2 0 0 0 0 0 0 0 0 0 0 5
3
4 0 0 2 1 4 1 3 1 0 0 0 0 0 0 0 0 3
-1
Алканы (также насыщенные углеводороды, парафины, алифатические соединения) — ациклические углеводороды линейного или разветвленного строения, содержащие только простые связи. Алканы являются насыщенными углеводородами и содержат максимально возможное число атомов водорода. Каждый атом углерода в молекулах алканов находится в состоянии sp3-гибридизации — все четыре гибридные орбитали атома С идентичны по форме и энергии, четыре связи направлены в вершины тетраэдра под углами  . Cвязи C–C представляют собой σ-связи, отличающиеся низкой полярностью и поляризуемостью.
. Cвязи C–C представляют собой σ-связи, отличающиеся низкой полярностью и поляризуемостью.
Ничего не поняв, вы обратились к однокласснику за помощью. Он сказал вам забыть всё, что было написано в учебнике, и объяснил, что алканы — углеводороды. То есть соединения, состоящие из атомов углерода и водорода, не содержащие связей водород–водород, причём каждый углерод соединен ровно с четырьмя другими атомами, а каждый водород соединен ровно с одним другим атомом. При этом алкан является связным соединением, а также молекула алкана не является цикличной (для каждых двух атомов существует единственный способ добраться из одного в другой по связям между атомами). Также он сказал, что связи между атомами всегда соединяют два различных атома.
Запомнив всё это, вы пошли к Александру Евгеньевичу, и он дал вам задание: для данного соединения определить, является ли оно алканом.
В первой строке содержатся два числа N и M (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 100 000) — количество атомов и соединений между атомами соответственно.
Следующая строка состоит из N символов. Если i-й символ — «C», то i-й атом — атом углерода. Если i-й символ — «H», то i-й атом — атом водорода. Гарантируется, что каждой символ этой строки — либо «C», либо «H».
В следующих M строках содержатся описания соединений между атомами. В i-й из них содержатся номера двух атомов, связанных i-м соединением.
Выведите «YES», если соединение является алканом, и «NO», если не является.
8 7
HHHCCHHH
1 4
2 4
3 4
4 5
5 6
5 7
5 8
YES
2 1
CH
1 2
NO
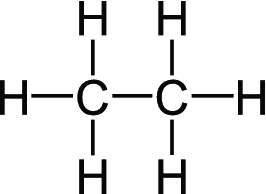
Соединение в первом примере является молекулой этана. Ниже представлена его структурная формула.
Телекоммуникационная сеть крупной IT-компании содержит n серверов, пронумерованных от 1 до \(n\). Некоторые пары серверов соединены двусторонними каналами связи, всего в сети m каналов. Гарантируется, что сеть серверов устроена таким образом, что по каналам связи можно передавать данные с любого сервера на любой другой сервер, возможно с использованием одного или нескольких промежуточных серверов.
Множество серверов \(A\) называется отказоустойчивым, если при недоступности любого канала связи выполнено следующее условие. Для любого не входящего в это множество сервера \(X\) существует способ передать данные по остальным каналам на сервер \(X\) хотя бы от одного сервера из множества \(A\).
На рис. 1 показан пример сети и отказоустойчивого множества из серверов с номерами 1 и 4. Данные на сервер 2 можно передать следующим образом. При недоступности канала между серверами 1 и 2 — с сервера 4, при недоступности канала между серверами 2 и 3 — с сервера 1. На серверы 3 и 5 при недоступности любого канала связи можно по другим каналам передать данные с сервера 4.
Требуется написать программу, которая по заданному описанию сети определяет следующие числа: \(k\) — минимальное количество серверов в отказоустойчивом множестве серверов, \(c\) — остаток от деления количества способов выбора отказоустойчивого множества из \(k\) серверов на число \(10^9 + 7\)
Первая строка входного файла содержит целые числа \(n\) и \(m\) — количество серверов и количество каналов связи соответственно (\(2 \le n \le 200000\), \(1 \le m \le 200000\)). Следующие \(m\) строк содержат по два целых числа и описывают каналы связи между серверами. Каждый канал связи задается двумя целыми числами: номерами серверов, которые он соединяет.
Гарантируется, что любые два сервера соединены напрямую не более чем одним каналом связи, никакой канал не соединяет сервер сам с собой, и для любой пары серверов существует способ передачи данных с одного из них на другой, возможно с использованием одного или нескольких промежуточных серверов.
Выведите два целых числа, разделенных пробелом: \(k\) — минимальное число серверов в отказоустойчивом множестве серверов, \(c\) — количество способов выбора отказоустойчивого множества из \(k\) серверов, взятое по модулю \(10^9 + 7\)
В приведенном примере отказоустойчивыми являются следующие множества из двух серверов: {1, 3}, {1, 4}, {1, 5}.
Баллы за каждую подзадачу начисляются только, если все тесты для этой подзадачи и всех необходимых подзадач успешно пройдены.
5 5 1 2 2 3 3 4 3 5 4 5
2 3
Петар организует вечеринку по случаю своего дня рождения и планирует пригласить некоторых сотрудников из компании, где он работает генеральным директором. Каждый сотрудник, включая Петара, имеет уникальный номер от 1 до N и тип шуток, которые он рассказывает, V i . Также, каждый сотрудник в компании кроме Петара имеет ровно одного начальника. Так как Петар - генеральный директор компании, он имеет номер 1 и руководит всеми сотрудниками (не обязательно напрямую).
На вечеринке есть некоторые правила, которым должны отвечать все присутствующие: 1. На вечеринке не должно быть двух людей с одинаковым типом шуток. 2. Человек не может быть приглашен на вечеринку, если на нее не приглашен его прямой начальник. 3. Человек не может быть приглашен на вечеринку, если типы шуток, которые рассказывает он и его приглашенные подчиненные, не образуют последовательное множество.
Петар хочет знать, сколько возможных наборов типов шуток может быть на его вечеринке, если он пригласит людей в соответствии с вышеуказанными правилами.
Последовательное множество - такое множество, в котором, если отсортировать его по возрастанию, разность между соседними элементами будет равна 1. Например (3, 1, 2) и (5, 1, 2, 4, 3) - последовательные множества, а (2, 5, 3) - нет.
Первая строка содержит одно целое число N ( 1 ≤ N ≤ 10000 ). Вторая строка содержит N целых чисел V i - типы шуток, рассказываемые i -м человеком ( 1 ≤ V i ≤ 100 ). Каждая из следующих N - 1 строк содержит два целых числа A и B ( 1 ≤ A , B ≤ N ), обозначающих что сотрудник с номером A является прямым начальником сотрудника с номером B .
Выведите единственное число - количество возможных наборов типов шуток на вечеринке.
4 2 1 3 4 1 2 1 3 3 4
6
4 3 4 5 6 1 2 1 3 2 4
3
6 5 3 6 4 2 1 1 2 1 3 1 4 2 5 5 6
10
Вы наверняка слышали легенду о Короле Артуре и Рыцарях Круглого Стола. Практически все версии этой истории указывают на то, что круглость Круглого Стола тесно связана с верой Артура в равенство среди рыцарей. Это ложь! На самом деле выбор Артура касательно формы стола вызван его детской травмой.
В реальности Артур был принужден убирать и мыть квадратные столы с юного возраста после того как на них играли в бирюльки. После соревнований по этой игре обычно на столе остается множество палочек, не касающихся друг друга. В духе соревнования, организаторы установили свод строгих правил для уборщиков. Точнее, палочки со стола должны быть убраны одна за другой путем их сдвига к ближайшему к уборщику краю стола. Они не должны вращаться и касаться других палочек в процессе перемещения.
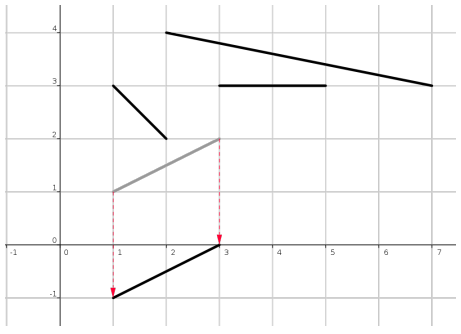
В этой задаче представим стол на координатной плоскости как квадрат с противоположными вершинами в точках (0, 0) и (10000, 10000), где палочкам соответствуют прямые отрезки, лежащие внутри квадрата. Предположим, что Артур сидит у края стола, прилежащего к оси X. Тогда уборка палочек со стола сводится к передвижению их к оси X, покуда они не упадут со стола. Ваша задача - определить порядок уборки палочек со стола, который соответствует условиям из предыдущего абзаца.
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 5000 ) - количество палочек на столе. Каждая из следующих N строк содержит 4 целых числа x 1 , y 1 , x 2 , y 2 ( 0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 10000 ), обозначающих крайние точки палочек.
В единственной строке выведите N целых чисел - номера палочек в том порядке, в котором они должны быть убраны со стола. Если существует несколько решений, выведите любое из них.
4 1 3 2 2 1 1 3 2 2 4 7 3 3 3 5 3
2 4 1 3
4 0 0 1 1 1 2 0 3 2 2 3 3 4 0 3 1
4 3 1 2
3 4 6 5 5 2 1 15 1 3 2 8 7
2 3 1