Мосты(2 задач)
Применение обхода в глубину(3 задач)
Топологическая сортировка(2 задач)
Точки сочленения(1 задач)
Бойцовский клуб дебатов - необычный клуб во всех отношениях. Каждый из \(2^{n}\) его членов заполнил специальную анкету, содержащую \(n\) вопросов с бинарным ответом (да/нет) о своих взглядах. Ответы каждого человека могут быть представлены в виде последовательности из \(n\) бит, иначе говоря в виде числа от \(0\) до \(2^{n} - 1\).
Перечислим ещё несколько инетерсных фактов о бойцовском клубе дебатов.
В первой строке вводится число \(n\) (\(2 \le n \le 18\)) - количество вопросов в анкете.
В последующих \(2^{n - 1}\) строках даны пары людей. В \(i\) строке даны целые числа \(a_i\) и \(b_i\), разделённые одним пробелом - что означает, что люди, чьи анкеты закодированы числами \(a_i\) и \(b_i\) являются парой. Гарантируется, что каждое целое число от \(0\) до \(2^{n} - 1\) встретится во вводе ровно один раз.
Выведете строку со единственным словом 'NO' , если не существует рассадки членов клуба по местам удоволетворяющей условию.
Иначе, выведете в первой строке слово 'YES'. Во второй строке выведите \(2 ^ n\) чисел, разделённые пробелами, кодирующие ответы последовательных людей вокруг стола - корректную рассадку (стол круглый, поэтому можно начинать вывод с любого человека).
Если существует несколько решений, выведите любое.
В задаче оценка по подгруппам. Подгруппы отличаются значением \(n\). Для для \(n = 2\) - \(4\) балла за подгруппу, для каждого значения \(n\) от \(3\) до \(18\) по \(6\) баллов за подгруппу.
3 0 5 4 1 3 6 7 2
YES 0 5 7 2 6 3 1 4
Члены комиссии соревнования ICPC не смогли придумать задачи, поэтому они решили ранжировать команды лексикографически. Таким образом, победителем станет команда, название которой лексикографически самое маленькое. Героиня этой задачи, Этна, является лидером команды, личность которой мы будем скрывать. Название её команды начинается с буквы «Z», что ставит её в довольно плохое положение. После долгих разговоров с комитетом Этна смогла добиться более справедливого способа ранжирования команд. К сожалению, команды будут продолжать сортировать лексикографически, но определение лексикографического порядка изменится. А именно, комитет случайным образом выберет перестановку букв английского алфавита и определит лексикографический порядок, используя эту перестановку. Этна сразу же достала свой ноутбук и написала программу, которая находит перестановку букв для каждой команды, согласно которой эта команда выиграет соревнование. К сожалению, программа еще не закончена. Помогите Этне и напишите более эффективную программу с той же функциональностью.
На первной строке дано натуральное число \(N\), которое обозначает количество команд, участвующих в соревновании.
В следующих \(N\) строках даны названия команд, участвующих в соревновании. Название каждой команды состоит из одного слова, которое в свою очередь состоит из строчных букв английского алфавита. Конечно, названия команд отличаются друг от друга.
Для каждой команды в исходном порядке необходимо вывести перестановку букв английского алфавита, в соответствии с которой эта команда выиграет соревнование. Если такой перестановки нет, необходимо вывести слово «nemoguce», а если таких перестановок несколько, достаточно вывести любую.
В этой задаче 3 подгруппы. Обозначим \(L\) - суммарную длину строк, \(K\) - количество различных букв.
(13 баллов) \(1 \le N \le 100, 1 \le L \le 10000, 1 \le K \le 6\)
(32 балла) \(1 \le N \le 350, 1 \le L \le 10000, 1 \le K \le 26\)
(55 баллов) \(1 \le N \le 25000, 1 \le L \le 1000000, 1 \le K \le 26\)
3 war zag wro
yxwzvutsqponmlkjihgfedcbar zyxwvutsrqponmlkjihgfedcba yxwzvutsrqponmlkjihgfedcba
3 b ab aa
zyxwvutsrqponmlkjihgfedcba nemoguce zyxwvutsrqponmlkjihgfedcab
7 bcada dbaab bbabc ababb aacdf bcdff baddb
zyxwvutsrqponmlkjihgfecbad zyxwvutsrqponmlkjihgfedcba zyxwvutsrqponmlkjihgfebdca nemoguce zyxwvutsrqponmlkjihgfecadb zyxwvutsrqponmlkjihgfecbda nemoguce
Король Байтазар считает, что Байтотия — земля, полная красивых достопримечательностей — должна привлечь множество туристов, которые должны потратить много денег, которые в конечном счете должны найти свой путь в королевскую казну. Но реальность далека от мечты. Поэтому король поручил своему советнику изучить этот вопрос. Советник выяснило, что иностранцы держаться подальше от Байтотии из-за ее плохой дорожной сети. В Байтотии \(n\) городов соединенных \(m\) двусторонними дорогами. Не гарантируется, что от каждого города можно добраться от любого другого города. Советник отметил, что нынешний дорожная сеть не позволяет делать длительные путешествия. А именно, где бы вы не начали поездку, невозможно посетить более 10 городов не прохождения через какой-то город два раза. Из-за ограниченных средств в казне, новые дороги построить нельзя. Вместо этого, Байтазар решил создать сеть туристическо-информационных пунктов (ТИП), которые будут рекламировать короткие путешествия. Для каждого города должен быть ТИП либо в нем, либо в одном из городов, непосредственно связанных с ним дорогой. Кроме того, известна стоимость строительства ТИПа в каждом из городов. Помогите королю найти самый дешевый спосою построить ТИПы, так, чтобы это условие удовлетворялось.
Первая строка стандартного ввода содержит два целых числа \(n\) и \(m\) (\(2 \le n \le 20000, 0 \le m \le 25000\)), которые задают количество городов и дорог в Байтотии соответственно. Города нумеруются от \(1\) до \(n\). Вторая строка содержит целые числа \(c_i\) (\(0 \le ci \le 10000\)) — стоимости строительства ТИПов в городах. Затем идет описание дорожной сети. i-я строка содержит два целых числа \(a_i, b_i\), которые указывают, что города \(a_i\) и \(b_i\) связаны дорогой. Существует не более одной дороги между любой парой городов.
Выведите одно целое число — общую стоимость строительства всех ТИПов.
Подзадача 1 (22 балла): \(1 \le n, m \le 20\)
Подзадача 2 (78 баллов): Без дополнительных ограничений. Оценивается потестово. (6 баллов за тест)
6 6 3 8 5 6 2 2 1 2 2 3 1 3 3 4 4 5 4 6
7
Центр Гдынии расположен на острове посередине реки Кацза. Каждое утро тысячи машин едут из жилых районов на западном берегу в индустриальные на восточном.
Остров можно представить в виде прямоугольника \(A\times B\) со сторонами, параллельными осям координат, углами \((0, 0)\) и \((A, B)\).
На острове есть \(n\) перекрёстков, пронумерованных натуральными числами от \(1\) до \(n\). Перекрёсток номер \(i\) имеет координаты \((x_i, y_i)\). Если координаты какого-то перекрёстка имеют вид \((0, y)\), то он находится на западном берегу, если \((A, y)\) - на восточном. Перекрёстки соединены дорогами, каждая - отрезок на плоскости, они не пересекаются (кроме концов). Дороги бывают односторонними и двусторонними. Нет никаких мостов и туннелей! Некоторые дороги могут идти по краям прямоугольника.
Поскольку плотность траффика растёт, мэр города нанял Вас (кого же ещё) проверить, достаточно ли текущей сети дорог. Он попросил написать программу, которая по карте города определит для каждого перекрёстка на западном берегу, сколько из него достижимых на восточном.
В первой строке входных данных дано четыре целых числа \(n\), \(m\), \(A\) и \(B\) (\(1\leq n\leq 300 000\), \(0\leq m\leq 900 000\), \(1\leq A\leq 10^9\), \(1\leq B\leq 10^9\). Это количества перекрёстков, дорог и размеры города, соответственно.
В каждой из следующих \(n\) строк есть два целых числа \(x_i\), \(y_i\) (\(0\leq x_i\leq A\), \(0\leq y_i\leq B\)), описывающих координаты перекрёстка номер \(i\). Перекрёстки не совпадают.
Следующие \(m\) строк описывают дороги, каждая одну. Это описание состоит из трёх чисел: \(c_i\) - номер перекрёстка, откуда (\(1\leq c_i\leq n\)), \(d_i\) - куда (\(1\leq d_i\leq n\)), \(k_i\in\{1, 2\}\) - тип дороги (сколькосторонняя). Разные дороги соединяют разные неупорядоченные пары перекрёстков.
Есть хотя бы один перекрёсткок на западном берегу, из которого можно добраться хотя бы в один на восточном по дорогам.
Выведите для каждого перекрёстка на западном берегу в своей строчке количество достижимых из него перекрёстков на восточном берегу.
Выводите в порядке уменьшения \(y\)-координаты.
1. (30 баллов) \(n, m\leq 6 000\).
2. (70 баллов) \(n\leq 300 000\), \(m\leq 900 000\).
5 3 1 3 0 0 0 1 0 2 1 0 1 1 1 4 1 1 5 2 3 5 2
2 0 2
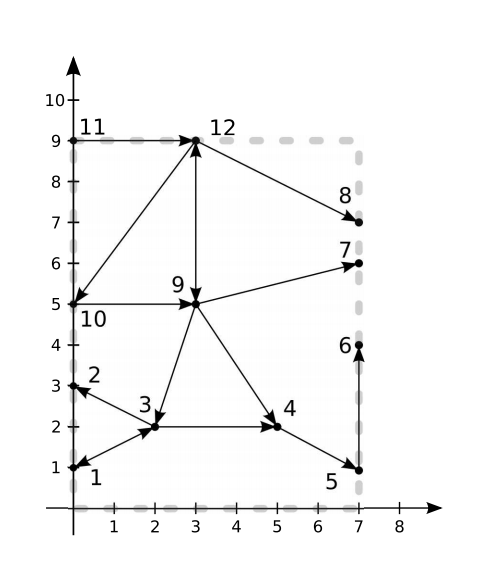
12 13 7 9 0 1 0 3 2 2 5 2 7 1 7 4 7 6 7 7 3 5 0 5 0 9 3 9 1 3 2 3 2 1 3 4 1 4 5 1 5 6 1 9 3 1 9 4 1 9 7 1 9 12 2 10 9 1 11 12 1 12 8 1 12 10 1
4 4 0 2
Поздравляем! Вас наняли управляющим одного крупного завода по производству чего-то очень важного. На вашем заводе есть \(n\) рабочих и \(n\) станков. Каждый рабочий умеет работать на каких-то станках, а на каких-то не умеет. К счастью, вы можете отправить какого-то рабочего на курсы повышения квалификации, чтобы он научился работать на каком-то станке, заплатив за это 1 тугрик. Нет никаких ограничений по тому, кого и сколько раз отправлять на курсы. У ваших работников также очень хорошая память, поэтому если они умели или научились работать на каком-то станке, то уже никогда не забудут, как это делать.
Но не все так радужно. Из-за кризиса сократили всех других менеджеров, поэтому рабочие сами определяют, за каким станком им работать в определенный день. Рабочие могут прийти на работу в случайном порядке. Когда рабочий пришел на работу он может выбрать любой еще не занятый станок, на котором умеет работать, и сядет за него. Если же такого не нашлось, то он расстроится и уйдет домой, а ваш завод понесет убытки. Так, если у вас было два рабочих, первый из которых умел работать на 1 и 2 станке, а второй только на первом, то если первый пришел на работу раньше и занял первый станок, то ваш завод понесет убытки.
Ваша задача в том, чтобы, потратив наименьшее кол-во тугриков на обучение сотрудников, сделать так, чтобы в каждый из дней все рабочие работали, а каждый станок был занят независимо от того, в каком порядке придут рабочие и какие станки они выберут.
В первой строке задано число \(1 \le n \le 25\) - кол-во рабочих и кол-во станков. Каждая из следующих строк содержит информацию об умениях рабочих. \(i+1\)-я строка ввода содержит строку \(s_i\), где \(s_{i,j} = 1\), если \(i\) рабочий умеет работать за \(j\)-м станком и 0 в обратном случае.
Выведите одно число - минимальное кол-во денег, которое вы можете потратить.
Подзадача 1(15 баллов) \(1 \le n \le 3\)
Подзадача 2(45 баллов) \(1 \le n \le 10\)
Подзадача 3(40 баллов) нет дополнительных ограничений
2 11 10
1
2 10 00
1
3 000 110 000
3