Мосты(2 задач)
Применение обхода в глубину(3 задач)
Топологическая сортировка(2 задач)
Точки сочленения(1 задач)
В некоторой стране есть развитая сеть железных дорог. С доисторических времён и до нашего времени в стране непрерывно происходят военные перевороты, из-за которых в системе железнодорожного транспорта этой страны происходят непрерывные изменения. Дело в том, что во время очередного переворота некоторые дороги разрушаются из-за военных действий, а пока новый правитель некоторое время находится у власти, он восстанавливает часть дорог.
Временами железнодорожная система в этой стране становилась довольно разветвленной, поэтому некоторые города могли быть соединены двумя и более дорогами. Кроме того, дорога могла начинаться и заканчиваться в одном и том же городе, причем для одного города таких дорог могло быть несколько.
Инженер Джио проводит испытания новых сверхскоростных поездов. Поскольку поезда экспериментальные, у них не должно возникать трудностей при проезде через промежуточные города. Поэтому инженер Джио требует, чтобы ни в каком городе на пути поезда, кроме, может быть, начального и конечного, не было развилок. Точнее, из любого промежуточного города на пути поезда должны выходить либо ровно две дороги, ведущие в другие города (возможно, в один и тот же), либо ровно одна дорога, начинающаяся и заканчивающаяся в этом городе.
Естественно, что Джио желает испытать поезд на максимальной возможной скорости, и поэтому после каждого изменения в системе путей он хочет знать максимальную длину пути, по которому может ехать поезд. Поскольку в доисторические времена не умели добывать железо, в начале никаких дорог между городами нет.
В первой строке входного файла находятся целые положительные числа \(n\) (1 ≤ \(n\) ≤ 500) – число городов в стране, и \(m\) (1 ≤ \(m\) ≤ 50 000) – число изменений в железнодорожной системе. В следующих \(m\) строках находится информация об изменениях состояния системы путей. Каждое изменение является либо добавлением дороги, либо удалением дороги. В случае добавления дороги в очередной строке записан ноль, а затем идут три целых числа. Первые два из них являются номерами городов, соединяемых дорогой, а последнее является длиной добавленной дороги. Города нумеруются целыми числам от 1 до \(n\). Длина дороги является целым положительным числом, не превосходящим \(10^6\). В случае удаления дороги в очередной строке сначала записана единица, а затем идёт номер шага, на котором произошло добавление удаляемой дороги. Шаги нумеруются целыми числами, начиная с 1.
Для каждого изменения системы путей выведите в очередную строку выходного файла символ `*', если после очередного изменения системы путей существует сколь угодно длинный путь, удовлетворяющий условиям, поставленным Джио. В противном случае выведите в выходной файл единственное целое число, являющееся длиной максимального возможного пути.
7 10 0 7 6 7 0 6 5 6 0 5 4 5 0 4 3 4 0 3 2 3 0 2 1 2 1 1 1 2 1 3 1 4
7 13 18 22 25 27 20 14 9 5
Ромин папа работает в стремительно развивающейся корпорации «РосКошки». Сегодня папа решил показать своему сыну свою компанию, ведь он планирует, что со временем все его дети и внуки будут работать в «РосКошках». Рома — мальчик любознательный, поэтому он довольно быстро узнал всё о структуре корпорации.
Всего в «РосКошках» работает N сотрудников, у каждого из которых (кроме президента) есть один непосредственный начальник. Чтобы сотрудники не отвлекались по мелочам, президент запретил им во время работы общаться с кем-либо, кроме своих непосредственных подчинённых и начальника. Поэтому все сообщения сотрудникам приходится передавать через других сотрудников. Пока Рома без дела бродил по коридорам фирмы, он не только узнал для каждого сотрудника, сколько ему требуется минут, чтобы передать сообщение одному из своих подчинённых или начальнику, но и обнаружил, что в этой фирме работает сисадмин, который имеет особый статус: у него нет ни начальников, ни подчинённых, и он может передавать сообщения любому сотруднику фирмы, причём мгновенно. Но при этом, если у сотрудника есть хотя бы один подчинённый, он никогда не подойдёт к сисадмину с просьбой передать сообщение кому-либо. Рома осознал, что только что ему открылся новый способ передачи информации внутри корпорации, поэтому разузнал для каждого сотрудника, не имеющего подчинённых, сколько ему требуется времени, чтобы дойти до сисадмина.
Ромин папа хорошо осознаёт масштабы любопытства своего сына, поэтому, когда ему в очередной раз потребовалось передать своему другу срочное сообщение, он обратился к своему сыну. Помогите Роме минимизировать время, необходимое для передачи папиного сообщения его другу.
В первой строке входного файла содержится единственное целое число \(N\) — количество сотрудников компании без учёта сисадмина (\(2 \le N \le 10^5\)). В следующих \(N\) строках содержится по 3 целых числа \(p_i\), \(b_i\) и \(s_i\) — номер начальника \(i\)-го сотрудника (для президента \(p_i=0\)) и время, необходимое для передачи сообщения от \(i\)-го сотрудника его начальнику и любому подчинённому соответственно. Если у \(i\)-го сотрудника нет подчинённых, то \(s_i\) — время, необходимое \(i\)-му сотруднику, чтобы добраться до сисадмина (\(1 \le p_i \le N\), \(p_i \ne i\), \(1 \le b_i\) , \(s_i \le 10^4\)).
Выведите единственное число — минимальное время, необходимое для доставки сообщения от Роминого папы (имеющего номер 1) до его друга (имеющего номер \(N\)).
Предприятие «Авто-2010» выпускает двигатели для известных во всём мире автомобилей. Двигатель состоит ровно из \(n\) деталей, пронумерованных от 1 до \(n\), при этом деталь с номером \(i\) изготавливается за \(p_i\) секунд. Специфика предприятия «Авто-2010» заключается в том, что там одновременно может изготавливаться лишь одна деталь двигателя. Для производства некоторых деталей необходимо иметь предварительно изготовленный набор других деталей.
Генеральный директор «Авто-2010» поставил перед предприятием амбициозную задачу — за наименьшее время изготовить деталь с номером 1, чтобы представить её на выставке.
Требуется написать программу, которая по заданным зависимостям порядка производства между деталями найдёт наименьшее время, за которое можно произвести деталь с номером 1.
Первая строка входного файла содержит число \(n\) (\(1\le n\le100000\)) — количество деталей двигателя. Вторая строка содержит \(n\) натуральных чисел \(p_1,p_2, \ldots,p_n\), определяющих время изготовления каждой детали в секундах. Время для изготовления каждой детали не превосходит \(10^9\) секунд.
Каждая из последующих \(n\) строк входного файла описывает характеристики производства деталей. Здесь \(i\)-я строка содержит число деталей \(k_i\), которые требуются для производства детали с номером \(i\), а также их номера. В \(i\)-й строке нет повторяющихся номеров деталей. Сумма всех чисел \(k_i\) не превосходит 200000.
Известно, что не существует циклических зависимостей в производстве деталей.
В первой строке выходного файла должны содержаться два числа: минимальное время (в секундах), необходимое для скорейшего производства детали с номером 1 и число \(k\) деталей, которые необходимо для этого произвести. Во второй строке требуется вывести через пробел \(k\) чисел — номера деталей в том порядке, в котором следует их производить для скорейшего производства детали с номером 1.
3 100 200 300 1 2 0 2 2 1
300 2 2 1
2 2 3 1 2 0
5 2 2 1
4 2 3 4 5 2 3 2 1 3 0 2 1 3
9 3 3 2 1
Рассмотрим расписание движения электричек на некоторой железнодорожной линии. Нас будут интересовать только электрички, идущие в одном направлении.
Каждая электричка отправляется с некоторой станции и следует до некоторой другой станции со всеми остановками. При этом средняя маршрутная скорость у каждой электрички своя (будем считать, что весь маршрут электричка проходит с этой скоростью, временем стоянки на станциях пренебрежем). Поскольку на участке только один путь в данном направлении — электрички в процессе следования друг друга не обгоняют.
Требуется выпустить книжку-расписание электричек. Обычно такая книжка представляет собой таблицу, где в первом столбце перечислены все станции, а каждый следующий столбец соответствует электричке: если электричка проходит через станцию, то в соответствующей клетке указывается время прохождения этой электрички через эту станцию, и прочерк, если электричка через эту станцию не проходит.
Естественно, что в книжке-расписании нужно расположить электрички так, чтобы они были указаны в хронологическом порядке. А именно, если две электрички имеют хотя бы одну общую станцию (даже если она является начальной станцией для одной, и конечной — для другой электрички), электрички в расписании должны идти в том порядке, в каком они проходят через эту станцию (поскольку электрички не обгоняют друг друга, то это же будет справедливо для всех общих станций этих двух электричек). Если же электрички не имеют ни одной общей станции, то они могут быть указаны в любом порядке.
По данному расписанию движения электричек определите порядок, в котором электрички должны идти в книжке—расписании.
Сначала вводится целое число N (1 ≤ N ≤ 1000) — количество электричек. Далее идёт описание электричек: каждая электричка задается четырьмя числами Ai, Bi, Ci, Di (0 ≤ Ai < Bi ≤ 106, 1 ≤ Ci ≤ 100, 0 ≤ Di ≤ 10000), которые обозначают, что данная электричка отправляется со станции «Ai-й километр» и следует до станции «Bi-й километр». Электричка отправляется с начальной станции в момент Ci. Один километр электричка проезжает за Di секунд.
Гарантируется, что расписание можно составить корректно, в частности, никакая электричка не обгоняет другую.
Выведите последовательность из N номеров от 1 до N – номера электричек в том порядке, в котором они должны идти в книжке-расписании. Если возможных ответов несколько, выведите любой.
Комментарий к примеру тестов
Ответ 2 3 1 также будет верным.
3 1 10 3 4 3 5 3 4 10 11 10 1
3 2 1
Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной \(w\) ячеек и высотой \(h\) ячеек. В некоторых из них расположены кнопки.
Код на этом замке вводится одновременным нажатием \(k\) кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.
Для оценки надежности замков требуется написать программу для вычисления указанной величины.
В первой строке входного файла находятся три целых числа \(h\), \(w\) и \(k\) (\(1\le h,w\le 30\); \(1\le k \le 10\)). Каждая из последующих \(h\) строк содержит \(w\) символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.
В выходной файл выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.
| Входные данные | Выходные данные |
|
2 2 2 #. ## |
2 |
5 6 7
|
3 |
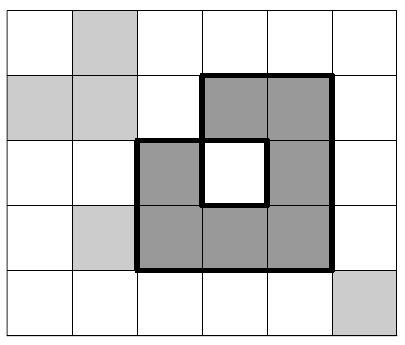
На рисунке изображен один из возможных кодов для второго примера.