Петя учится играть в шахматы. Недавно он заметил, что несмотря на то, что кони умеют прыгать через фигуры, они могут мешать друг другу дойти до нужных клеток. Петя поставил на доску двух коней: черного и белого, и для каждого их них выбрал клетку, на которой он хочет его видеть. Теперь ему интересно, какое минимальное число ходов потребуется коням, чтобы дойти до нужных клеток.

Кони ходят по шахматным правилам (на одну клетку по горизонтали и две по вертикали или на одну клетку по вертикали и на две по горизонтали). Порядок ходов черного и белого коня может быть произвольным. Коням не разрешается одновременно вставать на одну и ту же клетку.

Совсем недавно Али-Баба узнал от своего брата Касима об удивительной игре Го. В Го играют на прямоугольной доске – гобане, расчерченном вертикальными и горизонтальными линиями. Все линии пронумерованы. В игре участвуют два игрока, которые по очереди выставляют на гобан камни – специальные круглые фишки. Каждый камень ставится на незанятую точку пересечения линий доски (пересечения называют пунктами). У одного игрока – черные камни, у другого – белые. Камни одного цвета, смежные по вертикали, либо по горизонтали (но не диагонали), объединяются в группу. Одиночный камень также считается группой.

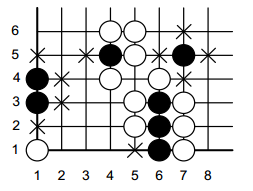
Один из способов набрать очки в Го – захватить камни противника. Каждый камень может иметь от двух до четырех смежных с ним пунктов (по вертикали и горизонтали, но не по диагонали). Если такой пункт не занят камнем, то он называется «дамэ». Дамэ группы – это все дамэ камней, составляющих группу. Как только оппонент своими камнями закрывает все дамэ чужой группы, то эта группа считается захваченной и снимается с доски. Если у группы осталось лишь одно дамэ, то говорят, что эта группа находится в «атари» т.е. на один шаг от захвата соперником.

Дамэ черных камней на рисунке отмечены крестиком. Группа черных из камней (1, 3) и (1, 4) имеет 4 дамэ. Группа (6, 1), (6, 2) и (6, 3) имеет одно дамэ и находится в атари. Черный камень (4, 5) также находится в атари. Помогите Али-Бабе, который всегда играет черными, определить, какие его группы находятся в атари.

Отделу космических исследований поступило задание сфотографировать из космоса \(n\) объектов в заданной области. Область имеет форму квадрата размером \(50\times 50\) километров. Если разделить ее на квадраты размером \(1\times 1\) километр, то интересующие отдел объекты окажутся в центрах некоторых единичных квадратов.

Введем систему координат, направив ось OX с запада на восток и ось OY с юга на север. Тогда каждому единичному квадрату будут сопоставлены координаты в диапазоне от 1 до 50, как показано на рисунке ниже.

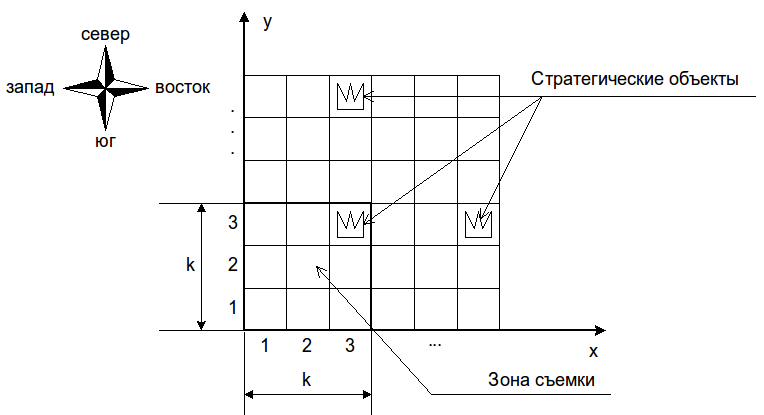
Для космической съемки используется специальный фотоаппарат высокого разрешения, установленный на космическом спутнике. Фотоаппарат может делать снимки квадратных участков земной поверхности размером \(k\times k\) километров. Исходно аппарат наведен на юго-западный угол заданной области, то есть, если сделать снимок, на нем будут видны единичные квадраты с координатами \(x\) и \(y\) от \(1\) до \(k\) километров.

С помощью специальных двигателей можно изменять орбиту спутника, что приводит к изменению участка съемки. За один день орбиту спутника можно изменить таким образом, что участок съемки сместится либо на один километр на запад, либо на один километр на восток, либо на один километр на север. Переместить участок съемки на юг невозможно. Непосредственно между перемещениями спутника можно сделать снимок, временем съемки можно пренебречь.

Руководство отдела заинтересовалось вопросом: за какое минимальное количество дней можно сделать снимки всех объектов заданной области.

Требуется написать программу, которая по заданному расположению объектов и размеру снимка \(k\) определит минимальное время, за которое можно сделать снимки всех объектов заданной области.