--->
54 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
| Максимальное время работы на одном тесте: | 5 секунд |
Неориентированный граф без петель и кратных ребер задан матрицей смежности. Определить, является ли этот граф деревом.
Входные данные
Сначала вводится число N – количество вершин графа (от 1 до 100). Далее записана матрица смежности размером N*N, в которой 1 обозначает наличие ребра, 0 – его отсутствие. Матрица симметрична относительно главной диагонали.
Выходные данные
Введите сообщение YES, если граф является деревом, и NO в противном случае.
Примеры
Входные данные
4 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 0
Выходные данные
YES
#410
Темы:
[Перебор с отсечением]
[Способы задания графа]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более, чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
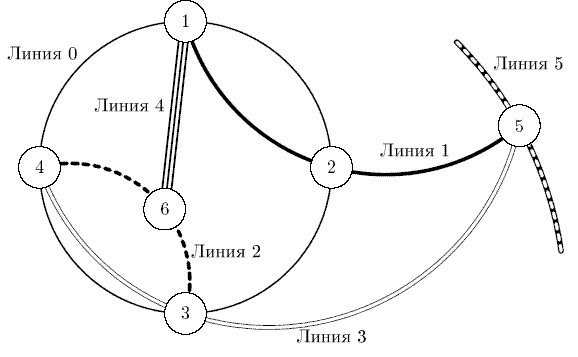
На рисунке приведена возможная схема метро, соответствующая второму примеру.
Входные данные
В первой строке вводится число k – количество линий метро в городе ( 1
k10). Все линии пронумерованы от 0 до k - 1, кольцевая линия имеет номер 0. Во второй строке записано число n – количество пересадочных станций. Каждая из следующих n строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Выходные данные
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
Примеры
Входные данные
4 6 2 0 1 2 0 2 2 0 3 2 0 1 2 0 2 2 0 3
Выходные данные
NO
Входные данные
6 6 3 0 1 4 2 0 1 3 0 2 3 3 0 2 3 3 1 3 5 2 2 4
Выходные данные
YES
#416
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Во Флатландии n городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание n - 1 шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды – числа от 1 до n.
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача – таким образом сопоставить числам от 1 до n города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
Входные данные
В первой строке вводится целое число n – количество городов во Флатландии ( 2n1500).
Далее следует n описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города – строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа x и y – координаты города. Координаты не превышают 104 по абсолютной величине.
Далее следуют n - 1 строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа – номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более, чем одним шоссе.
Выходные данные
Выведите n строк, i-я из этих строк должна содержать название города, который следует сопоставить числу i в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите строку «No solution».
Примеры
Входные данные
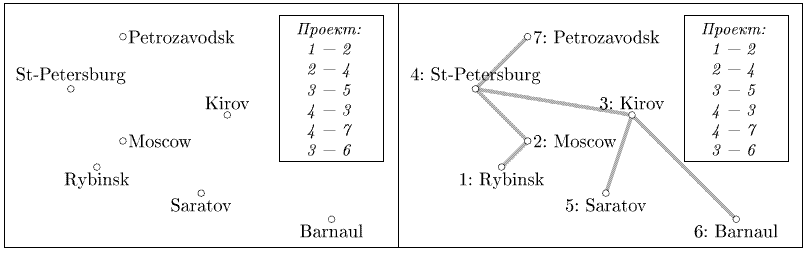
7 Moscow 2 2 St-Petersburg 0 4 Kirov 6 3 Saratov 5 0 Rybinsk 1 1 Petrozavodsk 2 6 Barnaul 10 -1 1 2 2 4 3 5 4 3 4 7 3 6
Выходные данные
St-Petersburg Rybinsk Kirov Saratov Moscow Petrozavodsk Barnaul
По заданной квадратной матрице n×n из нулей и единиц определите, может ли данная матрица быть матрицей смежности простого неориентированного графа.
Входные данные
На вход программы поступает число \(n\) \((1 \le n \le 100)\) – размер матрицы, а затем n строк по \(n\) чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите «YES», если приведенная матрица может быть матрицей смежности простого неориентированного графа, и «NO» в противном случае.
Примеры
Входные данные
5 0 0 1 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0
Выходные данные
YES
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
По заданной матрице смежности неориентированного графа определите, содержит ли он петли.
Входные данные
На вход программы поступает число n ( \(1 \le n \le 100\) ) – количество вершин графа, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите «YES», если граф содержит петли, и «NO» в противном случае.
Примеры
Входные данные
5 1 1 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0
Выходные данные
YES
Выбрано
:
|