Темы --> Информатика --> Алгоритмы --> Динамическое программирование --> Динамическое программирование: два параметра --> Динамическое программирование на таблицах
---> 46 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#79
Арбузная грядка
  
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
64 megabytes

Ограничение по времени:        3 секунды
Ограничение по памяти:         64 мегабайта

На этот раз Вася увлекся выращиванием арбузов. Его огород имеет форму прямоугольника \(N \times M\) метров, разделенного на одинаковые ячейки размером \(1 \times 1\) метр, в каждой из которых растет по арбузу. Как-то раз он решил  осмотреть некоторые из них, начав в левом верхнем углу, пройдясь по огороду и вернувшись обратно. Ячейки, оказавшиеся внутри цикла, считаются осмотренными, остальные – не осмотренными. По некоторым банальным соображениям Вася не ходит по грядкам, а только лишь по специальным дорожкам, расположенным на границах ячеек с арбузами. Вдобавок, он хочет, чтобы его путь получился без самопересечений. К счастью, дорожки достаточно широкие для того, чтобы гулять по ним много раз, не считая это за самопересечение (см. рисунки к примерам).

Ваша задача – узнать, за какое минимальное время Васе удастся обойти ровно i арбузов. Можно считать, что он двигается равномерно со скоростью 1 метр в секунду.

Формат входных данных 

В первой строке входных данных содержатся два числа \(N, M (1 \le N, M \le 50)\). В следующих N строках идет описание огорода. В (i + 1)-й строке содержатся M символов. Символ "I" на j-й позиции означает, что Вася хочет осмотреть арбуз, расположенный в i-й строке и j-м столбце огорода; символ " ." означает, что ему не важно, что происходит в соответствующей ячейке; символ "X" означает, что он не хочет осматривать это растение. Других символов в строке нет.

Гарантируется, что  суммарное количество символов "I" и "X" не превосходит 10, и присутствует хотя бы один символ "I".

Формат выходных данных 

Выведите ровно K чисел, разделенных пробелами, где K – количество арбузов, которые Вася хочет осмотреть (количество символов "I" во входном файле). Число номер i должно быть равно минимальному времени, за которое он успеет осмотреть ровно i арбузов, соответствующих символам "I".

Не забудьте учесть, что арбузы, помеченные ".", могут быть осмотрены или нет, но арбузы "X" Вася осматривать не хочет ни в коем случае.

Примеры

Входные данные

Выходные данные

1 1
I             

4

2 2
XX
XI

8
Рис. 1

3 3
III
IXI
III

4 6 8 10 12 14 16 18
Рис. 2

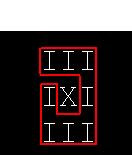
3 3
X. I
.I.
I..

8 10 14

1 10
IIXIIXIXII

4 6 12 14 20 26 28

#206
Обход таблицы
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

В прямоугольной таблице NxM в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.

Входные данные

Вводятся два числа N и M - размеры таблицы (1<=N<=10, 1<=M<=10).

Выходные данные

Выведите искомое количество способов.

Примечание

При указанных ограничениях число способов входит в тип Longint.

Примеры
Входные данные
1 10
Выходные данные
1
#313
Биномиальные коэффициенты
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Для биномиальных коэффициентов (числа сочетаний из n по k) хорошо известна рекуррентная формула: Cnk=Cn-1k-1+Cn-1k, Cn0=Cnn=1.

Входные данные

Вводится 2 числа - \(n \le 20 \) и \( k \le 20 \).

Выходные данные

Необходимо вывести  значение Cnk.

Примеры
Входные данные
4 2
Выходные данные
6
#317
Число сочетаний
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

По данным натуральным n и k вычислите значение \(C_n^k = \frac{n!}{k!(n-k)!}\) (число сочетаний из n элементов по k).

Входные данные

Вводятся 2 числа - n и k (\(n, k \leq 10\)).

Выходные данные

Необходимо вывести  значение \(C_n^k\).

Примеры
Входные данные
2
1
Выходные данные
2
#409
Максимальная сумма
  
Источники: [ Командные олимпиады, ВКОШП, 2006, Задача G ]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Задана таблица, содержащая числа. Необходимо найти прямоугольную рамку (прямоугольник, с осями, параллельными осям координат и шириной линий 1) с максимальной суммой чисел в ячейках, покрытых рамкой.

Сегодня на страницах газеты «Математический досуг» была опубликована необычная математическая головоломка. Одна из страниц газеты полностью занята прямоугольной таблицей, состоящей из m строк и n столбцов. В каждой ячейке таблицы записано некоторое целое число.

Для решения головоломки требуется найти такой невырожденный прямоугольник с вершинами в центрах ячеек таблицы, и сторонами, параллельными сторонам таблицы, чтобы сумма чисел, записанных в ячейках на границе получившегося прямоугольника, была максимальна.

Рис. 1

Безуспешно потратив несколько часов на решение головоломки, Саша решил написать программу, которая сделала бы это за него. Но и тут его постигла неудача. Теперь ему ничего не остается, как обратиться за помощью к вам.

Напишите программу, которая по заданной таблице найдет искомый прямоугольник.

Входные данные

В первой строке вводятся два целых числа \(m\) и \(n\) (\(2 \le m, n \le 300\)). Далее следует описание таблицы – \(m\) строк, каждая из которых содержит по \(n\) целых чисел \(a_{i, j}\) (\(-10^4 \le a_{i,j} \le 10^4\)).

Выходные данные

В первой строке  выведите целое число \(s\) – максимальную сумму чисел на границе искомого прямоугольника. Во второй строке выведите четыре натуральных числа: \(x_1\), \(y_1\), \(x_2\), \(y_2\) – координаты левой верхней и правой нижней ячейки выбранного прямоугольника, соответственно (здесь \(x\) – номер строки, а \(y\) – номер столбца, строки нумеруются сверху вниз, начиная с единицы, столбцы нумеруются слева направо, начиная с единицы). Если оптимальных решений несколько, выведите любое.

Примеры
Входные данные
2 3
1 1 1
1 1 1
Выходные данные
6
1 1 2 3
Входные данные
5 4
9 -2 -1 3
-10 -5 1 -4
1 -1 2 -2
3 0 0 -1
2 2 -1 2
Выходные данные
8
3 1 5 3
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест