В кабинете информатики есть старый стековый калькулятор. Он содержит K ячеек памяти, организованных в виде стека. Первая ячейка называется вершиной стека. На индикаторе калькулятора отображается содержимое вершины стека, если стек непуст.

Над стеком может выполняться операция проталкивания. Применение этой операции приводит к записи числа на вершину стека. Перед этим, если в стеке уже были числа, то каждое из них перемещается в ячейку с номером на единицу больше. Если в стеке уже находится K чисел, то выполнение операции проталкивания невозможно.

Калькулятор позволяет выполнять арифметические операции. Они применяются к числам, хранящимся во второй и первой ячейках стека. Результат операции записывается в первую ячейку стека, а число из второй ячейки удаляется. После этого, если третья ячейка непуста, то число из неё переписывается во вторую, если есть число в четвертой ячейке — оно переписывается в третью и так далее до последней занятой ячейки, которая становится пустой. Для выполнения арифметической операции в стеке должно быть хотя бы два числа. Например, при выполнении операций сложения или умножения, значения соответственно суммы или произведения чисел из первой и второй ячеек помещаются на вершину стека. Операция вычитания выполняется так: из содержимого второй ячейки стека вычитается содержимое первой ячейки.

Известно, что калькулятор неисправен. Из цифровых клавиш работает только клавиша «1». Нажатие этой клавиши приводит к проталкиванию в стек числа 1. Например, попытка набрать число 11, два раза нажав клавишу «1», приводит к тому, что в стек два раза проталкивается число 1. Из операций работают только сложение (клавиша «+»), умножение (клавиша «*») и вычитание (клавиша «-»). Если в результате вычитания получено отрицательное число, то калькулятор зависает.

Легко заметить, что на индикаторе возможно получить произвольное натуральное число. Например, чтобы получить число 3, необходимо дважды нажать клавишу «1», затем клавишу «+» (на индикаторе после этого появится число 2), затем один раз нажать клавишу «1» и один раз — клавишу «+». При K > 2 того же результата можно достичь иначе, трижды нажав клавишу «1», а затем два раза клавишу «+». Дополнительно используя операции умножения и вычитания, в некоторых случаях число N можно получить быстрее, чем сложив N единиц.

Требуется написать программу, которая определяет, каким образом можно получить на индикаторе калькулятора заданное число N, выполнив минимальное количество нажатий клавиш. Стек изначально пуст.

Знаменитый художник Вася только что закончил работу над своим новым шедевром и хочет знать, сколько он сможет получить за свой труд.

Картина представляет собой прямоугольник N на M сантиметров, разделенный на маленькие квадратики 1 на 1 сантиметр со сторонами, параллельными сторонам картины. Для достижения гармонии каждый из этих квадратиков Вася покрасил одним из 26 особых цветов, обозначаемых маленькими латинскими буквами.

Стоимость картины в точности равна количеству «симпатичных» частей в ней. Частью картины называется любой прямоугольник, который может быть вырезан из нее по границам квадратиков. Часть называется «симпатичной», если при выполнении симметрии относительно ее центра получается прямоугольник, раскрашенный также, как и исходная часть. Например, в картине, раскрашенной так:

abc
acb

симпатичными являются все части, состоящие из одного квадратика (их 6), а также части

bc и a

cb и a

Напишите программу, которая по информации о шедевре Васи определит его стоимость.

Для заданного числа \(n\) найдите наименьшее положительное целое число с суммой цифр \(n\), которое делится на \(n\).

У Олега есть матрица целых чисел \(N \times M\). Его очень часто просят узнать сумму всех элементов матрицы в прямоугольнике с левым верхним углом (\(x_1\), \(y_1\)) и правым нижним  (\(x_2\), \(y_2\)). Помогите ему в этом.

Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить только так, как показано на рисунке:

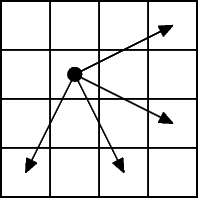
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.