Страница: << 8 9 10 11 12 13 14 >> Отображать по:
#946
Ход конем
  

Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить ТОЛЬКО на две клетки вниз и на одну клетку вправо, либо на две клетки вправо и на одну клетку вниз (смотри рисунок).

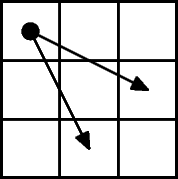
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.
 

Входные данные

В первой строке входного файла находятся два натуральных числа N и M (1 ≤ N, M ≤ 50).  

Выходные данные

В выходной файл выведите единственное число количество способов добраться конём до правого нижнего угла доски.

Примеры
Входные данные
4 4
Выходные данные
2
#992
Маскарад
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Есть N магазинов, для каждого из них задана цена метра, количество метров необходимых для "оптовой" покупки, цена метра при покупке оптом, а также имеющееся в магазине количество ткани. Необходимо купить L метров за минимальную цену (можно покупать в различных магазинах кусками).

По случаю введения больших новогодних каникул устраивается великий праздничный бал-маскарад. До праздника остались считанные дни, поэтому срочно нужны костюмы для участников. Для пошивки костюмов требуется L метров ткани. Ткань продается в N магазинах, в которых предоставляются скидки оптовым покупателям. В магазинах можно купить только целое число метров ткани. Реклама магазина номер i гласит "Мы с радостью продадим Вам метр ткани за Pi бурлей, однако если Вы купите не менее Ri метров, то получите прекрасную скидку — каждый купленный метр обойдется Вам всего в Qi бурлей". Чтобы воплотить в жизнь лозунг "экономика страны должна быть экономной", правительство решило потратить на закупку ткани для костюмов минимальное количество бурлей из государственной казны. При этом ткани можно купить больше, чем нужно, если так окажется дешевле. Ответственный за покупку ткани позвонил в каждый магазин и узнал, что:

1) реклама каждого магазина содержит правдивую информацию о ценах и скидках;

2) магазин номер i готов продать ему не более Fi метров ткани.

Ответственный за покупку очень устал от проделанной работы и поэтому поставленную перед ним задачу «закупить ткань за минимальные деньги» переложил на своих помощников. Напишите программу, которая определит, сколько ткани нужно купить в каждом из магазинов так, чтобы суммарные затраты были минимальны.

Входные данные

В первой строке входного файла записаны два целых числа N и L (1≤N≤100, 0≤L≤100). В каждой из последующих N строк находится описание магазина номер i — 4 целых числа Pi, Ri, Qi, Fi (1≤Qi≤Pi≤1000, 1≤Ri≤100, 0≤Fi≤100).

Выходные данные

Первая строка выходного файла должна содержать единственное число — минимальное необходимое количество бурлей.

Во второй строке выведите N чисел, разделенных пробелами, где i-ое число определяет количество метров ткани, которое нужно купить в i-ом магазине. Если в i-ом магазине ткань покупаться не будет, то на i-ом месте должно стоять число 0. Если вариантов покупки несколько, выведите любой из них.

Если ткани в магазинах недостаточно для пошивки костюмов, выходной файл должен содержать единственное число -1.

Примеры
Входные данные
2 14
7 9 6 10
7 8 6 10
Выходные данные
88
10 4
Входные данные
1 20
1 1 1 1
Выходные данные
-1
#1017
Еловая аллея
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Заданы координаты клеток на прямой, в которые можно посадить ели. Для каждого сорта ели определены тени, отбрасываемые на восток и на запад. Ели не могут расти в тени других елей. Требуется высадить как можно больше елей и для каждой занятой клетки указать, какой сорт ели будет туда посажен.

Мэр города Урюпинска решил посадить на главной аллее города, которая проходит с запада на восток, голубые ели. Причем сажать ели можно не во всех местах, а только на специально оставленных при асфальтировании аллеи клумбах.

Как оказалось, голубые ели бывают M различных сортов. Для ели каждого сорта известна максимальная длина ее тени в течение дня в западном и в восточном направлении (Wi и Ei соответственно). При этом известно, что ели растут гораздо лучше, если в течение дня они не оказываются в тени других елей.

Координатная ось направлена вдоль аллеи с запада на восток.

По заданным координатам клумб вычислите максимальное число елей, которое можно посадить, соблюдая условие о том, что никакая ель не должна попадать в тень от другой ели.

Входные данные

Во входном файле записано сначала натуральное число M — количество сортов елей (1M100). Затем идет M пар чисел Wi, Ei, описывающих максимальную длину тени в западном и восточном направлении в течение дня для каждого сорта ели (числа Wi, Ei — целые, из диапазона от 0 до 30000). Далее идет натуральное число N — количество клумб, в которых можно сажать ели (1N100). Далее идет N чисел, задающих координаты клумб (координаты — целые числа, по модулю не превышающие 30000). Клумбы перечислены с запада на восток (в порядке возрастания их координат).

Примечание

Если на клумбе с координатой X мы посадили ель, максимальная тень которой в восточном направлении равна E, то все клумбы с координатами от X+1 до X+E–1 попадают в тень от этой ели, а клумба с координатами X+E — уже нет. Аналогично для тени в западном направлении.

Выходные данные

В выходной файл выведите сначала число A — максимальное количество елей, которые удастся посадить, а затем A пар чисел, описывающих ели. Первое число каждой пары задает номер клумбы, в которую садится ель. Второе число определяет номер сорта этой ели.

Примеры
Входные данные
3
10 1
2 2
1 10
10
0
1
3
5
7
9
11
13
15
16
Выходные данные
8
9 2
8 2
7 2
6 2
5 2
4 2
3 2
1 2
#1020
Левый лабиринт
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

В спортзале размером NxM метров построили современный аттракцион под названием "Левый лабиринт". Для этого на полу спортзала с интервалом в 1 метр начертили линии, параллельные стенам спортзала. Таким образом, спортзал разбили на NxM клеток. Дальше некоторые из этих клеток покрасили в черный цвет.

Аттракцион заключается в том, что участника ставят в некоторой клетке спортзала и просят как можно быстрее добежать до некоторой другой клетки. При этом накладываются следующие условия:

  • Участнику запрещено ходить по черным клеткам.
  • Придя в какую-то клетку, участник может пойти либо прямо, либо налево, либо направо (если в соответствующем направлении клетка не покрашена в черный цвет): ходить назад, а также ходить по диагонали запрещается.
  • За все время пути участнику разрешается повернуть направо (то есть пойти из текущей клетки направо относительно того, откуда он пришел в данную клетку) не более K раз.
  • В начальной клетке участник может встать лицом в ту сторону, в какую ему захочется. С какой стороны участник прибежит в конечную клетку также не важно.

Известно, что на то, чтобы перебежать из клетки в соседнюю, участник тратит ровно 1 секунду. Требуется вычислить минимальное время, за которое участник сможет достичь конечной клетки.

Входные данные

Во входном файле сначала записано число K — количество разрешенных поворотов направо (целое число из диапазона от 0 до 5), затем записаны числа N и M, задающие размеры спортзала — натуральные числа, не превышающие 20. Далее записано N строк по M чисел в каждой. Число 0 обозначает непокрашенную клетку, число 1 — покрашенную, число 2 — клетку, откуда стартует участник и число 3 — клетку, куда нужно добежать (клетки, помеченные 2 и 3 являются непокрашенными). В лабиринте всегда есть ровно одна начальная клетка и ровно одна клетка, в которую нужно попасть.

Выходные данные

В выходной файл выведите минимальное время, за которое можно добраться в конечную клетку. Если попасть в конечную клетку с соблюдением всех условий нельзя, выведите –1.

Примеры
Входные данные
1 3 4
0 0 2 0
0 1 1 0
0 0 3 0
Выходные данные
6
Входные данные
0 5 5
0 1 0 0 0
0 1 0 1 0
0 0 3 1 0
1 0 1 1 0
2 0 0 0 0
Выходные данные
12
#1022
Анаграммер
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Анаграммер — специальное устройство для получения из слова его анаграмм (то есть слов, записанных теми же буквами, но в другом порядке). Это устройство умеет выполнять 2 операции:

  1. Взять очередную букву исходного слова и поместить ее в стек.
  2. Взять букву из стека и добавить ее в конец выходного слова.

Стек — это хранилище данных, которое работает по принципу "первый пришел — последний ушел". Стек можно представить себе в виде пирамидки. Когда мы добавляем букву в стек, это соответствует тому, что на стержень пирамидки сверху мы надеваем кольцо, на котором написана соответствующая буква. Когда берем букву из стека, то это соответствует тому, что мы снимаем со стержня верхнее кольцо, и смотрим, какая буква на нем написана.

Например, слово TROT в слово TORT может быть преобразовано анаграммером двумя различными последовательностями операций: 11112222 или 12112212.

Напишите программу, которая по двум заданным словам вычисляет количество различных последовательностей операций анаграммера, которые преобразуют первое из этих слов во второе, а также находит сами эти последовательности.

Входные данные

Первая строка входного файла содержит исходное слово, а вторая — слово, которое необходимо получить. Слова состоят только из заглавных латинских букв и имеют длину не более 50 символов. Оба слова имеют одинаковую длину. В этих строках не содержится пробелов.

Выходные данные

В первой строке выходного файла должно содержаться количество последовательностей операций анаграммера, с помощью которых можно преобразовать первое слово во второе.

Если это количество не превышает 1000, то в последующих строках должны содержаться сами последовательности. Каждая последовательность должна быть выведена на отдельной строке, и состоять из цифр 1 и 2 (указывающих порядок выполнения операций), выведенных без пробелов.

Примеры
Входные данные
TORT
TROT
Выходные данные
2
11112222
12112212
Входные данные
MOSCOW
OMCOWS
Выходные данные
1
112211212122
Страница: << 8 9 10 11 12 13 14 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест