Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
На новой станции метро, которую планируют открыть в конце этого года, будет N эскалаторов (эскалаторы пронумерованы подряд числами от 1 до N). Эскалаторы имеют длину L и расположены на расстоянии H друг от друга. Шириной эскалатором пренебрежем. Между каждыми двумя соседними эскалаторами (точно посередине) будет установлен ряд ламп. В ряду будет K ламп. Лампы устанавливаются по следующему принципу: всю длину эскалатора L разбивают на K равных отрезков и в середине каждого отрезка устанавливают по лампе (см. рисунок). Всего будет установлено (N–1)*K ламп.
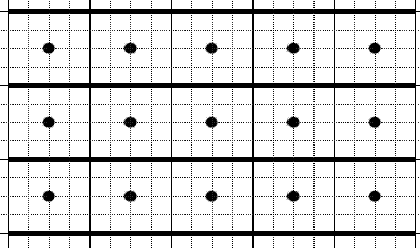
На приведенном рисунке N=4 (эскалаторы показаны жирными <горизонтальными линиями), L=20, H=4, K=5.
Васе удалось проникнуть на эту станцию еще до ее открытия, и даже прокатиться на эскалаторе. Он выбрал эскалатор номер J. Посчитайте, в скольких точках эскалатора (включая его начало и конец) Вася будет видеть не все лампы (так как их будут загораживать другие лампы).
Во входном файле записаны числа N, L, H, K, J. Все числа — натуральные. 2≤N≤35, 1≤L≤1000, 1≤H≤1000, 1≤K≤35, 1≤J≤N.
В выходной файл выведите одно число — ответ задачи.
2 20 4 5 1
0
4 20 4 5 2
11
Петя достаточно давно занимается в математическом кружке, поэтому он уже успел не только правила выполнения простейших операций, но и такое достаточно сложное понятие как симметрия. Для того, чтобы получше изучить симметрию Петя решил начать с наиболее простых геометрических фигур – треугольников. Он скоро понял, что осевой симметрией обладают так называемые равнобедренные треугольники. Поэтому теперь Петя ищет везде такие треугольники.
Напомним, что треугольник называется равнобедренным, если его площадь положительна, и у него есть хотя бы две равные стороны.
Недавно Петя, зайдя в класс, увидел, что на доске нарисовано n точек. Разумеется, он сразу задумался, сколько существует троек из этих точек, которые являются вершинами равнобедренных треугольников.
Требуется написать программу, решающую указанную задачу.
Входной файл содержит целое число n (3 ≤ n ≤ 1500). Каждая из последующих строк содержит по два целых числа – xi и yi – координаты i-ой точки. Координаты точек не превосходят 109 по абсолютной величине. Среди заданных точек нет совпадающих.
В выходной файл выведите ответ на задачу.
Разбалловка для личной олимпиады
Тесты 1-2 — из условия. Оцениваются в 0 баллов.
Тесты 3-13 — n не превосходит 500. Группа тестов оценивается в 40 баллов.
Тесты 14-28 — дополнительных ограничений нет. Группа тестов оценивается в 60 балла (вместе с предыдущими группами — 100 баллов).
Баллы начисляются за прохождение всех тестов группы и всех тестов предыдущих групп. При выставлении баллов за отдельные тесты каждый тест (кроме тестов из условия) оценивается в 4 балла.
3 0 0 2 2 -2 2
1
4 0 0 1 1 1 0 0 1
4
Как известно, при распространении радиоволн возникает интерференция, поэтому если рядом расположены две радиопередающие станции, вещающие на одной и той же частоте, то качество радиопередач резко снижается.
Радиостанция «Байтик» планирует транслировать свои программы в стране Флатландия. Министерство связи Флатландии выдало радиостанции лицензию на вещание на двух различных частотах.
Владельцы радиостанции имеют возможность транслировать свои радиопрограммы с использованием N радиовышек, расположенных в различных точках страны. Для осуществления трансляции на каждой радиовышке требуется установить специальный передатчик – трансмиттер. Каждый передатчик можно настроить на одну из двух частот, выделенных радиостанции. Кроме частоты вещания, передатчик характеризуется также своей мощностью. Чем мощнее передатчик, тем на большее расстояние он распространяет радиоволны. Для простоты, предположим, что передатчик мощности R распространяет радиоволны на расстояние, равное R километрам.
Все передатчики, установленные на вышках, должны, согласно инструкции министерства, иметь одну и ту же мощность. Чтобы программы радиостанции могли приниматься на как можно большей территории, мощность передатчиков должна быть как можно большей. С другой стороны, необходимо, чтобы прием передач был качественным на всей территории Флатландии. Прием передач считается качественным, если не существует такого участка ненулевой площади, на который радиоволны радиостанции «Байтик» приходят на одной частоте одновременно с двух вышек.
Требуется написать программу, которая определяет, какую максимальную мощность можно было установить на всех передатчиках, позволяющую выбрать на каждом передатчике такую одну из двух частот передачи, чтобы прием был качественным на всей территории Флатландии.
Первая строка содержит число N — количество вышек (3 ≤ N ≤ 1200). Последующие N строк содержат по два целых числа — координаты вышек. Координаты заданы в километрах и не превышают 104 по модулю. Все точки, в которых расположены вышки, различны. Все числа в строках разделены пробелом.
В первой строке выводится вещественное число — искомая мощность передатчиков. Во второй строке выводятся N чисел, где i-е число должно быть равно 1, если соответствующий передатчик должен вещать на первой частоте, и 2, если на второй. Ответ должен быть выведен с точностью, не меньшей 10–8.
4 0 0 0 1 1 0 1 1
0.707106781186548 1 2 2 1
Одна серьезная организация (ОСО) решила построить очень охраняемый объект (ООО). Для этого она нашла на пустыре два одиноко стоящих прожектора. Каждый из прожекторов освещает какой-то угол, меньший 180 градусов. ОСО хочет, чтобы весь ООО был освещен обоими прожекторами.
Положения прожекторов и освещаемые ими углы заданы. Требуется найти максимальную площадь ООО, который удастся построить.
Возможна ситуация, что ООО может иметь сколь угодно большую площадь. Однако если это не так, то гарантируется, что в этом случае максимальная возможная площадь не будет превышать 1015.
Во входном файле последовательно заданы описания двух прожекторов. Каждый из прожекторов описывается следующим образом: сначала идут координаты прожектора, а затем — координаты двух точек: по одной точке на каждой из сторон угла, освещаемого им. Все числа целые, не превосходящие по модулю 10000.
Выведите максимально возможную площадь ООО с точностью не менее 3-х знаков после десятичной точки. Если ООО построить не удастся, выведите 0. Если ООО может иметь любую сколь угодно большую площадь, выведите число –1.
0 1 2 3 3 2 3 0 3 3 5 2
-1
0 1 2 3 3 2 3 0 3 3 -3 2
3.000000
0 1 2 3 3 2 3 0 3 -2 -3 2
0.000000
Просека — эта такая прямая линия, которая проходит через лес (то есть деревья есть как с одной стороны от этой линии, так и с другой), и при этом она не проходит ни через одно из деревьев леса, а также не касается деревьев. Будем говорить, что лес является дремучим, если в нем нет ни одной просеки.
На плане леса все деревья изображаются кругами. Никакие два круга не пересекаются и не касаются друг друга. Требуется по этому плану определить, является ли лес дремучим.
Во входном файле содержится сначала целое число N — количество деревьев (1N200). Затем идет N троек чисел, задающих деревья. Первые два числа задают координаты центра, а третье — радиус. Все данные задаются точно, и выражаются вещественными числами, не более чем с 2 знаками после десятичной точки, по модулю не превосходящими 1000.
В первой строке выходного файла должно содержаться сообщение YES, если лес является дремучим, и NO иначе. Во втором случае вторая строка выходного файла должна содержать координаты двух точек, через которые проходит просека. Все координаты нужно выводить с восемью знаками после десятичной точки, координаты не должны превышать 2000, и расстояние между выданными точками должно быть не меньше 100.
3
0.00 30.00 25.00
0.00 -30.00 25.00
40.00 0.00 16.00
NO
-833.3333340000 -552.7707973875
833.3333340000 552.7707973875
3
0.00 30.00 29.00
0.00 -30.00 29.00
40.00 0.00 19.00
YES