Миротворцы ООН в одной из горячих точек планеты обезвреживали минное поле следующим образом. Имея карту, на которой каждая мина задана своими декартовыми координатами, они, обратив внимание на то, что никакие 3 мины не лежат на одной прямой, протянули специальный шнур от мины к мине так, чтобы он образовал выпуклый многоугольник минимального периметра, при этом все остальные мины оказались внутри многоугольника. Обезвредив соединенные мины, они вновь протянули шнур по тому же принципу, и опять обезвредили соединенные шнуром мины. Так продолжалось до тех пор, пока очередной шнур оказалось невозможным протянуть, руководствуясь изложенными правилами. Сколько мин осталось обезвредить и сколько раз саперам приходилось протягивать шнур?
В первой строке входного файла записано целое число \(N\) (\(3 \leq N \leq 1000\)) – количество мин. Во второй строке записано \(2\times N\) целых чисел (\(N\) пар \(x_i\), \(y_i\)), описывающих координаты каждой мины (\(-32000 \leq x_i, y_i \leq 32000\)).
Выведите в выходной файл два целых числа через пробел - количество оставшихся мин и количество операций по натягиванию шнура.
9 0 0 0 8 6 8 6 0 1 1 1 7 5 7 5 1 3 2
1 2
Плоскость разбили на одинаковые прямоугольники размера \(M\times N\) со сторонами, параллельными осям координат, и вершинами, расположенными в точках (\(M\times i, N\times j\)), где \(i\) и \(j\) пробегают всевозможные целые числа. Пусть на этой плоскости задана точка \(P(x,y)\) с целочисленными координатами. Назовем расстоянием от точки \(P\) до некоторого прямоугольника наименьшее из расстояний от \(P\) до точек этого прямоугольника, включая его границу. В частности, расстояние от точки до прямоугольника, в котором она содержится, равно 0.
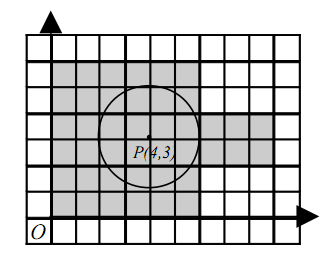Требуется написать программу, перечисляющую прямоугольники, удаленные от \(P\) на расстояние, не превосходящее \(L\). Прямоугольники должны быть перечислены в порядке неубывания этого расстояния.
Во входном файле содержатся целые числа \(M\), \(N\), \(L\), \(x\) и \(y\) (\(1 \leq M\leq 10\), \(1 \leq N\leq 10\), \(0\leq L\leq 1000\), \(–30000 \leq x,y \leq 30000\)), разделенные пробелами и/или переводами строк.
Выведите в выходной файл координаты левых нижних углов искомых прямоугольников в описанном выше порядке. Прямоугольники, равноудаленные от \(P\), могут выводиться в произвольном порядке.
3 2 2 4 3
7
На небе находится \(N\) облаков, и все они двигаются, под воздействием ветра, с постоянной скоростью \(v = (v_x, v_y)\). Т.е. для любого вещественного числа \(t \leq 0\) любая точка любого облака с начальными координатами \((x, y)\) переместится в точку (\(x + t \times v_x\), \(y + t \times v_y\)).
В нашей модели облака будут задаваться как многоугольники (включающие свою границу), вершины которых изначально имеют целые координаты. Многоугольники не имеют самопересечений и самокасаний. Облака могут пересекаться друг с другом.
На земле находится центр управления спутником (расположенный в точке (0, 0)), а ровно над ним, выше облаков, находится спутник. Центр осуществляет постоянный обмен данными со спутником с помощью лазерного луча. Когда на пути лазерного сигнала находится облако, коммуникация невозможна. В начальный момент времени коммуникация со спутником возможна. За время наблюдения может возникнуть несколько моментов, в которые коммуникация со спутником невозможна, когда луч лазера прерывается одним или несколькими облаками. Ваша задача состоит в том, чтобы написать программу, определяющую количество интервалов времени, когда коммуникация была невозможна.
В первой строке задано три целых числа \(N\), \(v_x\), \(v_y\) (\(1 \leq N \leq 1000\), \(-10^9 \leq v_x, v_y \leq 10^9\)), где \(N\) – количество облаков, а \(v_x\) и \(v_y\) задают скорость ветра. X-координата задает направление с запада на восток, а Y-координата – направление с севера на юг. Следующие N строк содержат описание облаков. Каждое облако описывается с помощью числа K (\(1 \leq K \leq 1000\)) – количества вершин, задающих облако, а также \(2\times K\) целых чисел – координаты вершин облака в порядке \(x_1\), \(y_1\), \(x_2\), \(y_2\), ..., \(x_N\), \(y_N\). Координаты по модулю не превосходят \(10^9\).
Выходной файл должна содержать единственное число – количество интервалов времени, в которые спутник был недоступен.
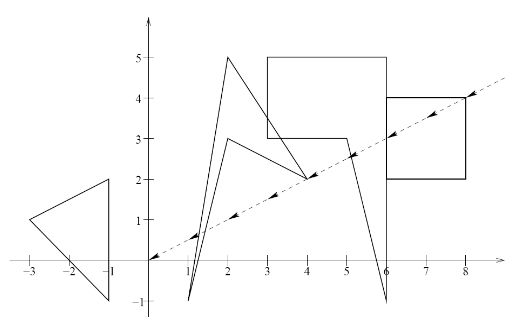
В данном примере центр управления два раза накрывается облаком 2 и один раз облаками 1 и 4.
4 -2 -1 4 6 2 6 4 8 4 8 2 4 2 3 1 -1 2 5 4 2 3 -3 1 -1 2 -1 -1 5 5 3 3 3 3 5 6 5 6 -1
3
Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.
Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:
\(x_0 < x_1 < x_2 < \dots < x_N\);
\(x_i = 0\) для некоторого \(0 < i < N\);
\(y_0 = y_N = 0\);
\(y_0 = y_N = 0\);
для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).
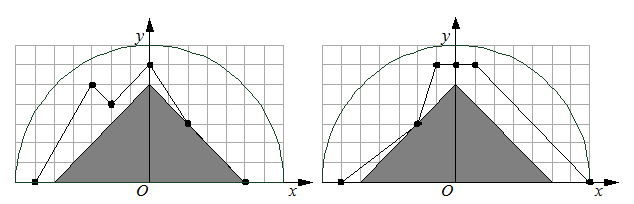
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:
основание треугольника лежит на оси абсцисс;
основание симметрично относительно начала координат;
треугольник полностью лежит внутри каждого из измеренных сечений заготовки.
Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.
Первая строка входного файла содержит целое число \(K\) – количество измеренных сечений.
Далее следуют описания каждого из \(K\) сечений. В первой строке описания сечения содержится число \(N_K\) – количество звеньев ломаной. За ней следуют (\(N_K + 1\)) строк, каждая из которых содержит пару целых чисел \(x_i\) и \(y_i\) – координаты вершин ломаной сечения в порядке их следования.
Выходной файл должен содержать одно вещественное число – наибольшую возможную площадь треугольника. Эта площадь должна иметь абсолютную или относительную погрешность не более \(10^{–6}\), что означает следующее. Пусть выведенное число равно \(x\), а в правильном ответе оно равно \(y\). Ответ будет считаться правильным, если значение выражения \(|x – y| / max(1, |y|)\) не превышает \(10^{–6}\).
Данная задача содержит пять подзадач.
\(K = 1\), \(N_1 \leq 15\), координаты вершин по модулю не превышают 20.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 20\), сумма \(N_i \leq 2000\), координаты вершин по модулю не превышают \(10^4\).
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\). Гарантируется, что полученный в качестве ответа треугольник является прямоугольным.
Для оценки данной подзадачи используется соответствующая группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.
\(1 \leq K \leq 1000\), сумма \(N_i \leq 10^5\), координаты вершин по модулю не превышают \(10^9\).
Каждый тест для данной подзадачи оценивается отдельно.
2 5 -6 0 -3 5 -2 4 0 6 2 3 5 0 5 -6 0 -2 3 -1 6 0 6 1 6 7 0
25.0
Кальпас — обычный говорящий пес, который живет в зоопарке на Марсе. К сожалению, условия содержания животных там не самые лучшие. Кальпаса выпускают на прогулку только раз в день, да и то, «выпускают» — не самое лучшее слово. Двое охранников: Вася и К-20071027, надевают на Кальпаса специальный ошейник и выводят его во двор. Ошейник полностью контролирует перемещения пса: в любой момент Кальпас находится в точности на середине отрезка между своими охранниками.
К сожалению, тот, кто изобрел этот ошейник, совершенно не думал о собаках. Как любому псу, Кальпасу хочется за время своей прогулки пробежать по строго определенному пути. Как же ему это сделать? Кальпас решил договориться со своими охранниками. Поскольку Вася — робот, который движется каждый день по заданному в его программе маршруту с постоянной скоростью, договориться с ним нет никакой возможности. Единственное, что остается Кальпасу — договориться с К-20071027.
Для того, чтобы подготовиться к переговорам, Кальпас хочет выяснить, путь какой длины должен пройти К-20071027, чтобы Кальпас двигался по намеченному пути с постоянной скоростью.
Входной файл содержит описание двух маршрутов, являющихся ломаными линиями: пути, по которому хочет пройти Кальпас и маршрута, по которому ежедневно ходит Вася.
Первая строка описания каждого из маршрутов содержит количество вершин ломаной, а последующие задают координаты этих вершин. Количество вершин в каждой ломаной не превышает 100, координаты точек целые и по модулю не превышают 1000.
В выходной файл выведите длину пути, который должен будет пройти К-20071027 с точностью не менее 10 - 6.
4 0 0 0 6 6 6 6 0 3 0 0 3 3 6 0
30.59411708155670700000