В городе N строят метро. Вася, житель города N, хочет знать, сколько станций окажутся недалеко от его дома. Помогите ему.
Город N отличается очень строгой планировкой улиц: каждая улица идёт либо строго с юга на север, либо строго с востока на запад; при этом расстояние между соседними параллельными улицами одинаково. Соответственно, в городе есть много перекрёстков, расположенных в вершинах квадратной сетки. По планам, первая линия метро будет прямой и будет иметь станции на каждом перекрёстке, через который она пройдёт. Вася считает, что станция находится недалеко от его дома, если расстояние по прямой от его дома до станции не превосходит некоторой фиксированной величины \(R\).
Введём систему координат с осью \(x\), направленной с востока на запад, и осью \(y\), направленной с юга на север, с началом координат на одном из перекрёстков и с единицей длины, равной расстоянию между соседними параллельными улицами. Таким образом, улицы будут прямыми с уравнениями ..., \(x=-2\), \(x=-1\), \(x=0\), \(x=1\), \(x=2\), ..., а также ..., \(y=-2\), \(y=-1\), \(y=0\), \(y=1\), \(y=2\), ...
Во первой строке входного файла находятся целые числа \(x_0\), \(y_0\) — координаты Васиного дома (считаем, что он находится на некотором перекрёстке), — и расстояние \(R\) в тех же единицах измерения, в которых введены координаты. Во второй строке находятся четыре числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) — координаты некоторых двух различных перекрёстков, через которые пройдёт линия метро. Все координаты во входном файле не превосходят \(100\,000\,000\) по модулю; расстояние \(R\) целое, положительное и не превосходит \(100\,000\,000\).
Можете считать, что линия метро будет бесконечной в обоих направлениях.
В выходной файл выведите одно число — количество станций, расположенных недалеко от Васиного дома.
Первый пример соответствует рисунку; на рисунке дом Васи и станции метро обозначены жирными
точками.
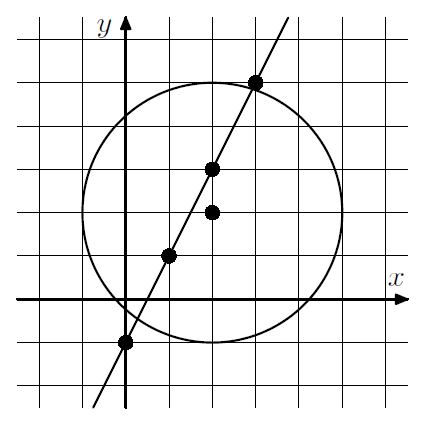
2 2 3 0 -1 1 1
2
0 0 1 -5 0 -3 0
3
Фирма, в которой всё ещё работает ваш друг, собирается расширяться на новые маршруты, и потому приобрела
новую площадку для ночного отстоя автобусов. Площадка раньше относилась к военной части, поэтому
она имеет необычную форму — форму треугольника, огороженного забором.
Для того, чтобы освещать площадку ночью, на ней надо установить несколько прожекторов. К счастью, у фирмы как раз в наличие есть три регулируемых прожектора, а на территории площадки обнаружились три высоких столба. Было решено на каждый столб повесить по прожектору и отрегулировать их так, чтобы каждый прожектор освещал ровно одну из трёх сторон забора: один прожектор должен освещать одну сторону забора, другой — другую, третий — третью. Никакой прожектор не должен освещать ни миллиметра “чужой” стены.
Конечно, прожекторы должны освещать не только забор, но вообще всю территорию площадки, поэтому возникла проблема: надо определить, какой прожектор на какую сторону забора направить. Зная ваши высокие навыки в решении подобных задач, фирма обратилась к вам за помощью. Напишите программу, которая будет решать эту задачу.
Естественно, каждый прожектор освещает не только стену, но и всю соответствующую часть двора — треугольник с вершиной в месте, где находится столб, на котором висит прожектор, и основанием, совпадающим с соответствующей стороной забора. Будем считать, что стороны этого треугольника тоже освещены прожектором. Тенью от столбов пренебрегайте.
Первая строка входного файла содержит одно число \(T\) — количество тестовых примеров, которые идут дальше (\(1\leq T\leq 1000\)).
Далее следуют описания \(T\) примеров. В каждом сначала идут шесть чисел \(x_1\), \(y_1\), \(x_2\), \(y_2\), \(x_3\), \(y_3\) — координаты вершин площадки, после чего идут шесть чисел \(X_1\), \(Y_1\), \(X_2\), \(Y_2\), \(X_3\), \(Y_3\) — координаты столбов. Гарантируется, что все столбы находятся строго внутри площадки. Гарантируется, что площадь площадки строго больше нуля. Гарантируется, что никакие два столба не совпадают. Все координаты во входном файле целые и не превосходят по модулю \(800\).
Выведите в выходной файл \(T\) строк по три числа в каждой: для каждого примера выведите номер стороны забора, на которую должен светить прожектор, находящийся на первом столбе, потом номер стороны, на которую должен светить прожектор со второго столба, и наконец номер стороны, на которую должен светить прожектор с третьего столба.
Первая сторона — та, которая соединяет вершины \((x_1, y_1)\) и \((x_2, y_2)\), вторая — \((x_2, y_2)\) и \((x_3, y_3)\), третья — \((x_3, y_3)\) и \((x_1, y_1)\).
Если решения не существует, выведите в соответствующую строку выходного файла три минус единицы:
“-1 -1 -1”.
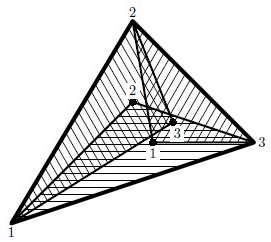
Первый пример соответствует рисунку.
Среди тестов будут такие, в которых \(T\leq 10\); суммарная стоимость таких тестов будет 70 баллов.
2 0 0 6 10 12 4 7 4 6 6 8 5 -10 -10 0 10 10 -10 0 1 0 -1 1 1
2 3 1 3 2 1
Реализуйте class LinEquation
На Международной олимпиаде по информатике некоторые участники, конечно же, получают удовольствие именно от решения предложенных задач, но большинство — от полученных в новой стране впечатлений. Впечатления принято запечатлевать на фотоаппарат. Участник T решил подойти к процессу съёмок с научной (по его мнению) точки зрения. Он находится на круглой обзорной площадке и желает заснять сразу два интересных объекта, местоположение каждого из которых на земле мы будем описывать с помощью отрезка. T выбирает точку для съёмок внутри этой площадки так, чтобы суммарная площадь двух треугольников, образованных концами соответствующих отрезков и выбранной точкой на обзорной площадке была как можно больше.
Помогите T с выбором такой точки. Возможность заснять сразу два объекта при этом анализировать не нужно, мы лишь действуем в рамках модели, сформулированной T. Если объекты загораживают друг друга, то этим также нужно пренебречь и считать площади независимо.
В первой строке входного файла находятся число T — количество тестов (1 ≤ T ≤ 105). Далее следуют описания тестов. В первой строке каждого описания содержится 4 числа x1, y1, x2, y2, характеризующие координаты концов первого отрезка. Во второй строке — x3, y3, x4, y4, описывающие второй отрезок. В третьей строке записаны три числа x0, y0, R — координаты центра круговой площадки и её радиус. Все числа целые, по модулю не превосходящие 1 000. Радиус положителен.
Гарантируется, что отрезки невырождены и не пересекаются с круговой площадкой. Также гарантируется, что они не имеют общих внутренних точек.
Для каждого теста выведите координаты точки внутри круга, удовлетворяющей условию задачи. Если таких точек несколько, то выведите любую из них. Координаты следует выводить с как можно бóльшим числом знаков после десятичной точки. Соответствующая сумма площадей должна отличаться от правильного ответа по абсолютной или относительной величине не больше чем на 10 - 6.
1
0 0 1 0
0 0 -1 0
0 2 1
0.0000000000 3.0000000000
После постройки станции метро Адмиралтейская, правительство Санкт-Петербурга решило построить по-настоящему глубокую станцию, которая будет самой глубокой в мире. Она будет расположена на глубине d метров под землей! Станция будет построена прямо под Смольным собором и будет предназначена для использования только должностными лицами. Департамент городского развития использует свою систему координат для этого проекта. Центром этой системы координат является Смольный собор и третья координата обозначает глубину. Соответственно, новая станция будет иметь координаты (0, 0, d).
Из-за соображений безопасности вестибюль станции должен быть расположен снаружи Смольного монастыря, в точке (x, y). Ваша задача — помочь правительству с постройкой эскалаторов. Станция будет использовать инновационные эскалаторы, которые идут вниз под углом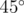 
. Возможна постройка промежуточного подземного вестибюля и двух эскалаторов. Вам даны x, y и d, найдите координаты промежуточного вестибюля. Заметьте, что вы не можете ничего строить на глубине, большей чем d, так что промежуточный вестибюль должен быть не глубже, чем основная станция.
Единственная строка входного файла содержит три целых числа: x, y и d — координаты вестибюля станции в системе Департамента городского развития и глубина станции ( - 10 000 ≤ x, y ≤ 10 000; (x, y) ≠ (0, 0); 106 ≤ d ≤ 10 000).
Выведите три числа с точностью не менее, чем 10 знаков после десятичной точки: координаты промежуточного вестибюля в системе координат Департамента городского развития.
Если невозможно построить эскалаторы, выведите "Impossible". Если промежуточный вестибюль не требуется, выведите "Single staircase".
0 100 300
0.0 200.0 100.0
300 400 500
Single staircase
400 400 500
Impossible