Геральд потратил несколько часов, рисуя прямоугольную сетку на листе бумаги. Сначала он нарисовал несколько вертикальных линий на одинаковом расстоянии dx между ними. После этого он нарисовал несколько горизонтальных линий. Они также находились на одинаковом расстоянии dy друг от друга.
Пока Геральд отдыхал от трудов, его брат Майк пришел и нарисовал прямую линию на листе бумаги. Геральд разозлился и приказал Майку стереть все лишнее с бумаги.
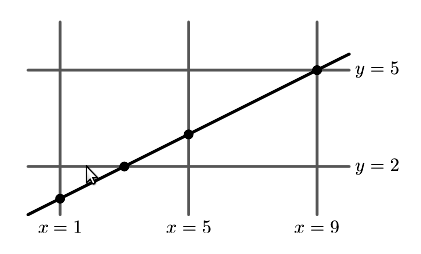
Но Майк не воспринял всерьез слова брата и стер все. Но он заметил, что точки пересечения его линии с сеткой были достаточно жирными для того, чтобы быть заметными даже после стирания.
Помогите Геральду восстановить параметры исходной сетки.
Первая строка входного файла содержит одно целое число n — количество точек пересечения (3 ≤ n ≤ 100 000).
Каждая из следующих n строк содержит два целых числа xi, yi — координаты одной из точек пересечения. Координаты не превосходят 109 по абсолютной величине.
Все точки пересечения различны. Других общих точек, кроме описанных выше, у сетки и прямой Майка нет.
Выведите шесть целых чисел x1, x2, dx, y1, y2 и dy. Первые три числа описывают набор вертикальных прямых: минимальная x-координата вертикальной прямой, максимальная x-координата вертикальной прямой и расстояние между соседними вертикальными линиями ( - 109 ≤ x1 ≤ x2 ≤ 109; 0 < dx ≤ 2·109). Следующие три числа аналогично описывают набор горизонтальных линий ( - 109 ≤ y1 ≤ y2 ≤ 109; 0 < dy ≤ 2·109).
Гарантируется, что хотя бы одно решение существует.
4
1 1
5 3
3 2
9 5
1 9 4 2 5 3
Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью небольших камушков. Митя разложил на поле n камушков так, чтобы каждый из них находился на одной из окружностей или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности размещался хотя бы один камушек. Обладая великолепным глазомером, Митя расположил камушки на окружностях абсолютно точно, без какой-либо погрешности.
На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем которого он был, то есть, восстановить окружности.
Требуется написать программу, которая по координатам камушков на поле находит вариант размещения их на двух несовпадающих окружностях.
Первая строка входного файла содержит целое число n — количество размещенных Митей камушков на поле (\(2 \leq n \leq 2000\)). Последующие n строк содержат целочисленные координаты (\(x_i\), \(y_i\)) камушков — по одной паре координат, разделенных пробелом, в каждой строке (\(−10^6 \leq x_i, y_i \leq 10^6\)). Никакие два камушка не размещаются в одной точке.
Гарантируется, что ответ для заданного набора камушков существует.
Выходной файл должен содержать две строки. Первая строка должна содержать последовательность номеров всех камушков, которые принадлежат первой окружности, вторая строка — последовательность номеров всех камушков, которые принадлежат второй окружности.
Каждый камушек должен встречаться хотя бы в одной из двух последовательностей. Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей. Считается, что камушки пронумерованы от 1 до n в порядке их следования во входных данных.
Нумерация окружностей не имеет значения, то есть выводить две последовательности можно в любом порядке. Числа в последовательностях можно также выводить в произвольном порядке. Каждая из последовательностей должна содержать не менее одного числа. Все числа в строках должны быть разделены пробелами.
Если вариантов расположения окружностей несколько, можно выбрать любой из них.
Правильные решения для тестов, в которых 2 ≤ n ≤ 50, будут оцениваться из 50 баллов.
7 1 -1 0 0 1 1 3 1 3 -1 2 0 4 0
1 2 3 6 4 5 6 7
5 -1000000 0 0 1000000 1000000 0 0 -1000000 0 0
1 2 3 4 5
На плоскости заданы дуга окружности, отрезок и точка. Как отрезок, так и дуга окружности непрозрачны. Определите, какая часть дуги видна из этой точки.
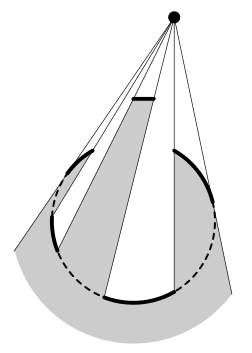
Входной файл состоит из трёх строк, описывающих данные объекты. Первая строка описывает дугу и содержит пять чисел — координаты центра дуги, радиус дуги, полярный угол точки начала дуги и полярный угол точки конца дуги. Полярные углы заданы в градусах
и отсчитываются относительно центра дуги против часовой стрелки от положительного направления оси \(x\). Вторая строка описывает точку и содержит два числа — её координаты. Третья строка описывает отрезок и содержит четыре числа — координаты
начала и конца отрезка. Все числа во входном файле вещественны и не превосходят \(10^6\) по модулю. Гарантируется, что как радиус окружности, так и длина отрезка больше нуля, что полярный угол конца дуги больше, чем полярный угол начала, и
что разность этих углов не превосходит 360.
Гарантируются, что никакие два из данных трёх объектов не имеют общих точек.
Выведите в выходной файл одно число на отрезке от 0 до 1 — относительную часть дуги, которая видна из данной точки. Ваш ответ должен отличаться от правильного не более, чем на 10−4.
2 1 2 120 420 3 6 2 4 2.5 4
0.496842552858631315
Компания, производящая оборудование для сотовой связи, обратилась к вам с просьбой написать программу, оценивающую качество организации сети. Одним из важных параметров является то, пересекаются ли зоны покрытия передатчиков, работающих на одинаковых частотах. Для простоты будем считать, что область покрытия каждого передатчика представляет собой многоугольник на плоскости (не обязательно выпуклый). Две области покрытия будем считать пересекающимися, если у них есть хотя бы одна общая точка (возможно, лежащая на границе одной или даже обеих областей). Ваша программа должна принимать на вход набор пар многоугольников, описывающих зоны покрытия передатчиков, и выводить про каждую пару информацию о том, пересекаются ли эти зоны.
На первой строке входного файла находится число K — количество тестов во входном файле. Далее идёт описание K тестов. Каждый тест задаётся описанием двух многоугольников, которые надо проверить на пересечение. Каждый многоугольник задаётся в следующем формате: сначала указывается одно число Ni — число вершин этого многоугольника, — после чего идут Ni строк, каждая из которых содержит два разделённых пробелом числа xij и yij — координаты j-й вершины этого многоугольника. Вершины перечислены в порядке обхода многоугольника.
Число пар многоугольников в одном тесте 1 ≤ K ≤ 10, число вершин каждого многоугольника 3 ≤ Ni ≤ 100, координаты вершин — целые числа, - 10 000 ≤ xij, yij ≤ 10 000.
Для каждой пары многоугольников выведите в выходной файл на отдельной строке одно слово: "YES", если многоугольники пересекаются, и "NO", если нет.
2 3 0 0 -1 0 0 -1 3 1 1 2 1 1 2 4 0 0 2 0 2 2 0 2 4 1 1 3 1 3 3 1 3
NO YES
Фирма, в которой работает ваш друг, недавно провела рекламную акцию «Сфотографируй маршрутку — получи приз», в рамках которой пассажиры могли присылать свои фотографии маршруток этой фирмы, а потом специальная конкурсная комиссия выбирала из них лучшие и награждала победителей. Теперь организаторы собираются выставить все фотографии на сайт фирмы.
При подготовке фотографий возникла одна проблема: видимо, некоторые пассажиры фотографировали маршрутки наспех, и потому некоторые фотографии оказались перекошенными: те линии, которые по идее должны быть горизонтальными, оказались наклонными (см. рис.). Администратор сайта категорически отказался выставлять такие фотографии на сайт, порекомендовав организаторам повернуть и обрезать фотографии так, чтобы горизонтальные линии стали на самом деле горизонтальными.
Поэтому организаторы провели большую работу и для каждой фотографии определили, под каким углом на фотографии наклонён горизонт. Теперь им надо вырезать из фотографии прямоугольник, у которого две стороны были бы параллельны горизонту, а две другие, конечно, перпендикулярны. Организаторы хотели вырезать прямоугольник наибольшей возможной площади, удовлетворяющий этому условию, но администратор сайта упростил им работу, потребовав сохранить отношение сторон фотографии. Таким образом, им теперь надо из каждой фотографии вырезать прямоугольный кусок со сторонами, параллельными и перпендикулярными горизонту, и с тем же отношением сторон, что и у оригинальной фотографии, причём среди всех таких прямоугольников выбрав наибольший по площади.
Зная вашего друга не только как хорошего экономиста, но и человека со связями, они обратились к нему с просьбой найти программу, которая помогла бы им выбрать нужный прямоугольник. Ваш друг перенаправил эту просьбу к вам.
Обратите внимание, что порядок сторон администратору сайта важен: если на оригинальной фотографии ширина была w, а высота h, а у найденного прямоугольника ширина (т. е. сторона, параллельная горизонту)w , а высота (т. е. вторая сторона) h, то должно быть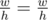 
, а не 
.
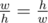Во входном файле находятся три вещественных числа: w, h и α — размеры оригинальной фотографии (ширина, высота) и угол наклона горизонта к ширине в градусах (см. рис.). Гарантируется, что 0 ≤ w ≤ 100, 0 ≤ h ≤ 100, - 90 ≤ α ≤ 90. Положительные α обозначают, что горизонт получается из ширины фотографии поворотом против часовой стрелки (как на рисунке), отрицательные α — по часовой стрелке.
В выходной файл выведите одно число — площадь искомого прямоугольника. Ваш ответ должен отличаться от правильного не более чем на 10 - 4.
4 3 30
5.1082415465
4 3.0 0
12.0000000000
4 3 90.0
6.7500000000