Винни Пух и Пятачок отправились воровать мед у пчел, и, в очередной раз влипли в неприятности. Пятачку опять потребовалось выстрелить из своего охотничьего ружья и пробить воздушный шарик, на котором Винни Пух поднялся к дуплу за медом. При этом желательно попасть именно в шарик, не задев медведя. Вычислите оптимальную позицию для стрельбы.

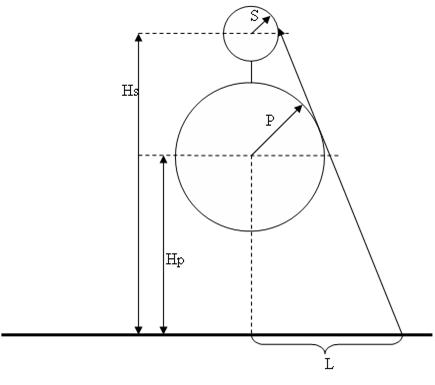
Поскольку Винни Пух очень любит покушать, то в данной задаче (да и не только в задаче) примем его за сферу радиуса  P. Центр медведя находится на высоте Hp над уровнем земли. Строго над медведем , находится еще одна сфера, радиуса S – воздушный шарик; центр шарика находится на высоте Hs над уровнем земли. Центры обеих сфер находятся на одной вертикальной прямой.  По понятным причинам гарантируется, что сферы не пересекаются J, однако могут касаться.

Считая, что ружье стреляет строго по прямой, вычислите минимальное расстояние L, на которое Пятачок должен отойти от места взлета, чтобы успешно поразить шарик. Шарик считается пораженным, если траектория пули хотя бы касается его поверхности; при этом если траектория пули касается медведя, то он считается невредимым.

На плоскости заданы N разных окружностей. Две окружности пересекаются, если они имеют хотя бы одну общую точку.

Напишите программу, которая по координатам центров окружностей и их радиусам найдет пару пересекающихся окружностей.

На территории будущей стройки растут три дерева. Фирма получила разрешение на строительные работы с условием, что два (любых) дерева будут сохранены. Прораб хочет построить забор треугольной формы так, чтобы внутри него оказалось ровно два дерева.

Деревья на плане изображаются кругами, которые попарно не вложены друг в друга и не пересекаются (но могут касаться).

Напишите программу, которая по введенной информации о деревьях определит, возможно ли построить такой забор, и, если да, то какое дерево окажется не огорожено.

Как известно, к северу от Москвы находится много горнолыжных трасс, расположенных на холмах Клинско-Дмитровской гряды. Один из курортов в связи с финансовым кризисом решил расширить спектр услуг, предлагая трассы для катания не только на лыжах и сноубордах, но и санные трассы.

У хозяев курорта имеется топографическая карта территории, высоты на которой отображены с помощью контуров, каждый из которых представляет собой окружность. У каждой окружности указана высота поверхности, прилегающей к внутреннему контуру этой окружности. Вся территория, которая не находится внутри какой-либо окружности, имеет высоту 0. Поскольку это единственная информация о местности, то можно условно считать, что участки между окружностями плоские. Никакие две окружности не пересекаются и не касаются.

Используя эту карту, необходимо проложить санную трассу, которая будет удовлетворять двум условиям: разница высот между начальной и конечной точками должна быть максимальна, и количество пересекаемых контуров не должно превышать некоторого заданного значения \(K\) (это связано с тем, что то место, которым сидят на санках, имеет ограниченную прочность). При этом трасса может иметь участки подъема, но не должна включать в себя ни одной точки, которая была бы выше начальной (туда санки просто не заедут).

На приведенном рисунке пунктирной линией показана наилучшая трасса для \(K\) = 4. Разница высот в ней составляет 68.