--->
144 задач
<---
Источники
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Пастбища Берляндии в опасности. Волки напали на пастбище овец. Пастух решил застрелить всех волков, при этом не убив ни одной овцы. Ружье заряжено бронебойными патронами, поэтому пули пролетают насквозь. Овцы и волки представлены отрезками. Пастух находится в точке (0, 0). Траектория полета пули — луч, выходящий из точки (0, 0). Если траектория пули имеет общуюточку с отрезком, характеризующим животное, то животное умирает. Найдите наименьшее количество выстрелов, необходимое для убийства всех волков. Овцы при этом должны остаться живы.
Входные данные
В первой строке записаны два целых числа N и M (0 ≤ N ≤ 100000, 0 ≤ M ≤ 100000) — количество волков и овец соответственно. Далее следует N+M строк. В каждой строке записано четыре числа X1, Y1, X2, Y2 (−1000 ≤ X1, X2 ≤ 1000, 1 ≤ Y1, Y2 ≤ 1000), описывающие отрезки. Первые N отрезков описывают положение волков, следующие M строк положение овец.
Выходные данные
Выведите наименьшее количество выстрелов, необходимое для убийства всех волков. Если невозможно убить всех волков, сохранив овец живыми, то выведите “No solution”.
Примеры
Входные данные
1 1 5 5 6 7 3 5 8 5
Выходные данные
No solution
Входные данные
2 1 1 1 2 3 -5 4 2 2 999 1000 1000 999
Выходные данные
1
Бинпоиск по углу. Пересекаем бублики и ГМТ из которых какие-нибудь две овцы видны под зафиксированным углом.
Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если \(A_1\) и \(B_1\) – образы некоторых точек \(A\) и \(B\) при движении, то \(|A_1 B_1| = |AB|\).
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой \(l\) и переноса на вектор, параллельный \(l\) (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
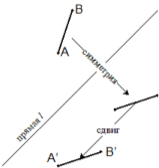
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии. Требуется по координатам двух различных точек \(A\) и \(B\) и двух точек \(A_1\) и \(B_1\), находящихся на таком же расстоянии друг от друга, как и точки \(A\) и \(B\), найти скользящую симметрию, переводящую точку \(A\) в точку \(A_1\), а точку \(B\) в точку \(B_1\).
Входные данные
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек \(A\) и \(В\). Во второй строке также находятся четыре целых числа – координаты двух различных точек \(A_1\) и \(В_1\). Гарантируется, что \(|A_1B_1| = |AB|\). Все числа во входном файле по модулю не превышают \(1000\). Числа в строках разделены пробелом.
Выходные данные
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой \(l\), относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.
ограничение по времени на тест
4.0 second;
ограничение по памяти на тест
256 megabytes
Роботы начинают все чаще использоваться в домашнем хозяйстве. Один программист решил сделать робота для своих хозяйственных нужд. Как известно, многие программисты потребляют напиток "Живчик", от которого на столе остаются разбросанные пустые бутылки. Поэтому он решил запрограммировать робота собирать пустые бутылки со стола.
Стол имеет форму прямоугольника длиной l и шириной w. Робот стартует в точке xr, yr, а N бутылок расположены в точках xi, yi (для i от 1 до N).
Чтобы убрать бутылку робот должен дойти до нее, взять ее, донести до любого края стола и сбросить. Робот может держать только одну бутылку, поэтому убирает он их по очереди.
Размером робота и бутылок можно пренебречь, в том числе можно считать что робот свободно может пройти мимо любой бутылки. Напишите программу, которая определяет минимальную длину пути робота, который ему необходимо пройти, чтобы убрать все бутылки со стола.
Входные данные
Первая строка входного файла содержит два целых числа w и l. (2 ≤ w, l ≤ 1000). Вторая строка входных данных содержит N – число бутылок на столе (1 ≤ N ≤ 18). Каждая из следующих N строк содержит два целых числа xi, yi – координаты i-й бутылки на столе (0<xi<w; 0<yi<l). Никакие две бутылки не находятся в одной точке.
Последняя строка входного файла содержит 2 целых числа xr, yr – координаты начальной позиции робота (опять же не у края стола и не в точке с бутылкой).
Выходные данные
Выведите длину кратчайшего пути робота с точностью не менее 6 значащих цифр после точки.
Примеры
Входные данные
3 4 2 1 1 2 3 2 1
Выходные данные
5.60555127546399
#2979
Темы:
[Элементарная геометрия]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Новый мэр крупного города Флатбурга Иван Котянин начал свою работу с решения проблем с пробками в городе. Как и в любом крупном городе, во Флатбурге есть кольцевая автодорога. Во Флатбурге она представляет собой монотонный многоугольник. Монотонным называется многоугольник, с которым каждая прямая, проходящая строго с севера на юг, имеет не более двух общих точек.
После совещания с правительством города было принято решение построить новую магистраль — скоростной диаметр, который вел бы строго с севера на юг и соединял две точки кольцевой автодороги.
Помимо борьбы с пробками решено было обновить рекорд по протяженности самой длинной магистрали, проложенной с севера на юг. Для того чтобы обновить рекорд необходимо построить магистраль длиной хотя бы \(d\) километров, а поскольку лишних денег в бюджете Флатбурга не так уж и много, решено было построить дорогу длиной ровно \(d\).
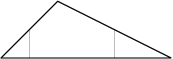
Министр транспорта Флатбурга решил предоставить мэру все варианты строительства новой дороги. Для начала он решил подсчитать, сколько существует способов построить магистраль. Помогите министру.
Входные данные
Первая строка входного файла содержит два целых числа \(n\) — количество вершин у многоугольника, задающего кольцевую автодорогу (\(3 \le n \le 100000\)), и \(d\) — длину новой магистрали (\(1 \le d \le 10^8\)).
Далее следует описание расположения вершин — каждая из следующих \(n\) строк содержит координаты \(x\) и \(y\) (\(-10^8 \le x, y \le 10^8\)) соответствующей вершины. Вершины заданы в порядке их обхода против часовой стрелки.
Направлению с севера на юг соответствуют прямые, задаваемые уравнением \(x = c\) для некоторого \(c\). Заданный многоугольник является монотонным.
Выходные данные
В выходной файл выведите количество способов построить дополнительную
магистраль длиной ровно \(d\). Если способов постройки бесконечно много,
выведите в выходной файл «Infinity».
Выбрано
:
|