--->
144 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
На плоскости даны две окружности. Ваша задача – найти все их общие точки.
Входные данные
В первой строке входного файла находится число \(K\) (\(1 \leq K \leq 10000\)) – количество пар окружностей. Каждая последующая пара строк описывает пару окружностей: в каждой строке записаны 3 целых числа \(x\), \(y\), \(r\) – координаты центра и радиус соответствующей окружности (\(-1000 \leq x,y \leq 1000\), \(0 < r \leq 1000\)).
Выходные данные
Для каждой пары окружностей вы должны вывети одну из следующих фраз: “There are no points!!!” – если окружности не пересекаются. “There are only i of them....” – если окружности пересекаются ровно в \(i\) точках. В этом случае последующие \(i\) строк должны содержать координаты точек пересечения в формате \(x\) \(y\). Точки должны быть выведены в лексикографическом порядке (сначала с меньшей координатой \(x\), а при равных \(x\) – сначала с меньшей \(y\)). Координаты следует выводить с 6 знаками после запятой. “I can't count them - too many points :(” – если точек пересечения бесконечно много. Все фразы должны быть выведены без кавычек. Вывод для каждой следующей пары окружностей должен быть отделен от предыдущего одной пустой строкой.
Примеры
Входные данные
2 0 0 2 4 0 2 0 0 1 1000 1000 1
Выходные данные
There are only 1 of them.... 2.000000 0.000000 There are no points!!!
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
На небе находится \(N\) облаков, и все они двигаются, под воздействием ветра, с постоянной скоростью \(v = (v_x, v_y)\). Т.е. для любого вещественного числа \(t \leq 0\) любая точка любого облака с начальными координатами \((x, y)\) переместится в точку (\(x + t \times v_x\), \(y + t \times v_y\)).
В нашей модели облака будут задаваться как многоугольники (включающие свою границу), вершины которых изначально имеют целые координаты. Многоугольники не имеют самопересечений и самокасаний. Облака могут пересекаться друг с другом.
На земле находится центр управления спутником (расположенный в точке (0, 0)), а ровно над ним, выше облаков, находится спутник. Центр осуществляет постоянный обмен данными со спутником с помощью лазерного луча. Когда на пути лазерного сигнала находится облако, коммуникация невозможна. В начальный момент времени коммуникация со спутником возможна. За время наблюдения может возникнуть несколько моментов, в которые коммуникация со спутником невозможна, когда луч лазера прерывается одним или несколькими облаками. Ваша задача состоит в том, чтобы написать программу, определяющую количество интервалов времени, когда коммуникация была невозможна.
Входные данные
В первой строке задано три целых числа \(N\), \(v_x\), \(v_y\) (\(1 \leq N \leq 1000\), \(-10^9 \leq v_x, v_y \leq 10^9\)), где \(N\) – количество облаков, а \(v_x\) и \(v_y\) задают скорость ветра. X-координата задает направление с запада на восток, а Y-координата – направление с севера на юг. Следующие N строк содержат описание облаков. Каждое облако описывается с помощью числа K (\(1 \leq K \leq 1000\)) – количества вершин, задающих облако, а также \(2\times K\) целых чисел – координаты вершин облака в порядке \(x_1\), \(y_1\), \(x_2\), \(y_2\), ..., \(x_N\), \(y_N\). Координаты по модулю не превосходят \(10^9\).
Выходные данные
Выходной файл должна содержать единственное число – количество интервалов времени, в которые спутник был недоступен.
Примечание
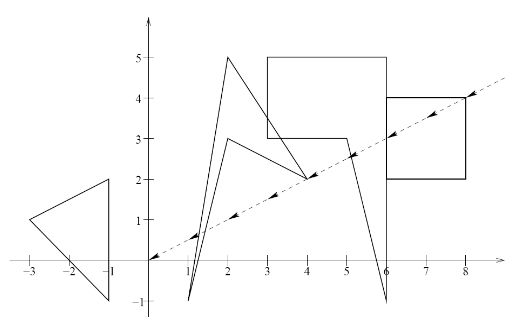
В данном примере центр управления два раза накрывается облаком 2 и один раз облаками 1 и 4.
Примеры
Входные данные
4 -2 -1 4 6 2 6 4 8 4 8 2 4 2 3 1 -1 2 5 4 2 3 -3 1 -1 2 -1 -1 5 5 3 3 3 3 5 6 5 6 -1
Выходные данные
3
#3411
Темы:
[Элементарная геометрия]
Источники:
[
Командные олимпиады,
Командные чемпионаты школьников Санкт-Петербурга по программированию,
2007,
Задача J
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Кальпас — обычный говорящий пес, который живет в зоопарке на Марсе. К сожалению, условия содержания животных там не самые лучшие. Кальпаса выпускают на прогулку только раз в день, да и то, «выпускают» — не самое лучшее слово. Двое охранников: Вася и К-20071027, надевают на Кальпаса специальный ошейник и выводят его во двор. Ошейник полностью контролирует перемещения пса: в любой момент Кальпас находится в точности на середине отрезка между своими охранниками.
К сожалению, тот, кто изобрел этот ошейник, совершенно не думал о собаках. Как любому псу, Кальпасу хочется за время своей прогулки пробежать по строго определенному пути. Как же ему это сделать? Кальпас решил договориться со своими охранниками. Поскольку Вася — робот, который движется каждый день по заданному в его программе маршруту с постоянной скоростью, договориться с ним нет никакой возможности. Единственное, что остается Кальпасу — договориться с К-20071027.
Для того, чтобы подготовиться к переговорам, Кальпас хочет выяснить, путь какой длины должен пройти К-20071027, чтобы Кальпас двигался по намеченному пути с постоянной скоростью.
Входные данные
Входной файл содержит описание двух маршрутов, являющихся ломаными линиями: пути, по которому хочет пройти Кальпас и маршрута, по которому ежедневно ходит Вася.
Первая строка описания каждого из маршрутов содержит количество вершин ломаной, а последующие задают координаты этих вершин. Количество вершин в каждой ломаной не превышает 100, координаты точек целые и по модулю не превышают 1000.
Выходные данные
В выходной файл выведите длину пути, который должен будет пройти К-20071027 с точностью не менее 10 - 6.
Примеры
Входные данные
4 0 0 0 6 6 6 6 0 3 0 0 3 3 6 0
Выходные данные
30.59411708155670700000
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Козла пустили в квадратный огород и привязали к колышку. Колышек воткнули точно в центре огорода. Козёл голоден, как волк, прожорлив, как бык, и ест всё, до чего дотянется, не перелезая через забор и не разрывая веревку. Какая площадь огорода будет объедена?
Входные данные
Длина стороны огорода и длина верёвки в метрах (положительные целые числа, не превосходящие 100, расположенные в одной строке через пробел).
Выходные данные
Площадь части огорода (в квадратных метрах, с точностью до 6 знаков после десятичной точки), объеденной козлом.
Примеры
Входные данные
10 6
Выходные данные
95.091113079
Выбрано
:
|