Фирма, в которой работает ваш друг, недавно провела рекламную акцию «Сфотографируй маршрутку — получи приз», в рамках которой пассажиры могли присылать свои фотографии маршруток этой фирмы, а потом специальная конкурсная комиссия выбирала из них лучшие и награждала победителей. Теперь организаторы собираются выставить все фотографии на сайт фирмы.
При подготовке фотографий возникла одна проблема: видимо, некоторые пассажиры фотографировали маршрутки наспех, и потому некоторые фотографии оказались перекошенными: те линии, которые по идее должны быть горизонтальными, оказались наклонными (см. рис.). Администратор сайта категорически отказался выставлять такие фотографии на сайт, порекомендовав организаторам повернуть и обрезать фотографии так, чтобы горизонтальные линии стали на самом деле горизонтальными.
Поэтому организаторы провели большую работу и для каждой фотографии определили, под каким углом на фотографии наклонён горизонт. Теперь им надо вырезать из фотографии прямоугольник, у которого две стороны были бы параллельны горизонту, а две другие, конечно, перпендикулярны. Организаторы хотели вырезать прямоугольник наибольшей возможной площади, удовлетворяющий этому условию, но администратор сайта упростил им работу, потребовав сохранить отношение сторон фотографии. Таким образом, им теперь надо из каждой фотографии вырезать прямоугольный кусок со сторонами, параллельными и перпендикулярными горизонту, и с тем же отношением сторон, что и у оригинальной фотографии, причём среди всех таких прямоугольников выбрав наибольший по площади.
Зная вашего друга не только как хорошего экономиста, но и человека со связями, они обратились к нему с просьбой найти программу, которая помогла бы им выбрать нужный прямоугольник. Ваш друг перенаправил эту просьбу к вам.
Обратите внимание, что порядок сторон администратору сайта важен: если на оригинальной фотографии ширина была w, а высота h, а у найденного прямоугольника ширина (т. е. сторона, параллельная горизонту)w , а высота (т. е. вторая сторона) h, то должно быть 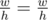 , а не
, а не 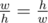 .
.
Во входном файле находятся три вещественных числа: w, h и α — размеры оригинальной фотографии (ширина, высота) и угол наклона горизонта к ширине в градусах (см. рис.). Гарантируется, что 0 ≤ w ≤ 100, 0 ≤ h ≤ 100, - 90 ≤ α ≤ 90. Положительные α обозначают, что горизонт получается из ширины фотографии поворотом против часовой стрелки (как на рисунке), отрицательные α — по часовой стрелке.
В выходной файл выведите одно число — площадь искомого прямоугольника. Ваш ответ должен отличаться от правильного не более чем на 10 - 4.
4 3 30
5.1082415465
4 3.0 0
12.0000000000
4 3 90.0
6.7500000000
В плоской стране все было как в настоящей, только плоское, и люди и горы и все, все, все. Жили в этой стране люди хорошие, но иногда попадались преступники и тогда их отвозили на плоский остров и там оставляли поразмыслить о жизни. А чтобы они не сбежали с острова, было решено построить наблюдательную вышку, с которой можно было бы следить за преступниками. Но, так как жители страны были плоскими, то и мозги у них были тоже плоскими и никак они не могли определить, в каком месте построить вышку и какой высоты. Помогите им. Вам предлагается найти самую низкую точку — координаты верхней точки вышки (плоские люди были экономными), из которой видно крайние точки острова, и найти высоту вышки. Как выяснили плоские ученые, профиль острова позволял построить вышку высотой не более 20000 метров. Профиль острова — это ломаная, имеющая примерно такой же вид как на рисунке. На острове нет лагун и с каждой вершины видны оба склона этой вершины. Точки С и Д — это крайние точки острова. 
Файл входных данных в первой строке содержит одно натуральное число N — количество вершин ломаной, не считая концов A и B. (1 ≤ N ≤ 1000) Во второй строке четыре целых числа x1, y1, x2, y2 — координаты точек A и B. ( - 1000 ≤ xi, yi ≤ 1000) В последующих N строках по два целых числа — координаты вершин xi, yi ломаной, данных в порядке обхода от А к В.( - 1000 ≤ xi, yi ≤ 1000)
Выходной файл должен содержать в первой строке два вещественных числа — координаты вершины вышки, во второй строке одно вещественное число — высоту вышки. Все числа с тремя знаками после десятичной точки. Если ответов несколько, то выведите самый левый из них.
3 0 0 100 0 20 20 40 20 70 30
50.000 50.000 26.667
«И молвил тогда Король: Ты храбро сражался, Рыцарь, и твой подвиг не будет забыт в веках. За доблесть твою я дарую тебе сей замок и земли вокруг него. Однако нарушен был тобой строжайший из запретов все войны видели, как ты сражался без Шляпы на голове подобно дикарям, и их злые духи могли вселиться в тебя. Ты знаешь, что закон предков велит отправлять на небеса души подобных тебе, пока зло, которое могло укорениться в них, не вырвалось наружу. Но в моей воле пощадить тебя, ибо я вижу, что ты достаточно силен чтобы не позволить этому злу проникнуть в мысли и душу твои. Ты должен дать обет три месяца и три дня не покидать своей земли и каждый день три часа после захода солнца молить добрых духов о защите. Дела торопят меня, и не могу я препроводить тебя до замка. Поэтому я дарую тебе и дорогу от этого места до замка. А сейчас иди, и возвращайся по истечении срока.»— так записано в Зеленой Книге Лет.
Помимо этого из Зеленой Книги Лет известно, что земли, вместе с которыми был дарован замок, имели форму круга. Король был очень мудр и, во избежание лишних разбирательств относительно права на землю всегда даровал только области земли, на карте имеющие выпуклую форму. Недавно в распоряжении историков оказалась информация о том, где располагался замок и где происходил этот исторический разговор. Их интересует, участок земли какой площади получил Рыцарь в предположении, что дорога до замка была идеально прямой.

Первая входного файла содержит два вещественных числа xk и yk координаты места, в котором происходил диалог. Во второй строке записаны три вещественных числа xc , yc и rc координаты замка и радиус окружности, ограничивающей дарованную вместе с ним землю. Все числа во входном файле по модулю не превосходят 10000.
В выходной файл выведите одно вещественное число — площадь земельного участка, полученного Рыцарем, с точностью не менее трех знаков после десятичной точки.
1440.82150 -499.96180 975.76735 -128.57330 297.57553
338836.3611315
Империя обнаружила мятежников на ледяной планете Хот! По сведениям разведки все командование Альянса Повстанцев сейчас скрывается на базе «Эхо», спрятанной в горах на севере этой суровой планеты.
Для того, чтобы окончательно подавить силы восстания, необходимо в ходе стремительной атаки уничтожить эту базу и скрывающихся на ней мятежников. К сожалению, укрытие хорошо укреплено: в частности, его защищает мощное силовое поле, препятствующее бомбардировкам с орбиты. Силовое поле имеет форму выпуклого многоугольника с вершинами в N специальных станциях-ретрансляторах. Никакие три станции не располагаются на одной прямой.
Перед тем как начинать операцию по уничтожению повстанцев, требуется лишить их базу силового поля, уничтожив эти N станций точечным бомбометанием. Однако точные координаты этих станций нам неизвестны. Ваша цель — узнать расположение станций-ретрансляторов, чтобы наши войска смогли начать наступление.
На планете введена система координат, устроенная таким образом, что все станции-ре-транс-ля-торы находятся в точках с целыми координатами, не превосходящими C по модулю.
В вашем распоряжении есть зонд-разведчик, оснащенный специальным оборудованием, позволяющим регистрировать станции-ретрансляторы. Если запустить его по прямой над базой повстанцев, по его информации можно будет узнать, сколько станций-ретрансляторов располагаются слева, и сколько — справа от прямой его движения. Станции, находящиеся на его пути, зонд не регистрирует.
С повстанцами надо расправиться как можно скорее: у вас есть время не более чем на 105 запусков этого зонда. Восстановите по полученной от него информации точные координаты станций-ретрансляторов, чтобы мы могли начать наступление, и Империя вас не забудет!
Это интерактивная задача.
При запуске решения на вход подаются два целых числа N (3 ≤ N ≤ 1 000) и C (5 ≤ C ≤ 1 000 000) — количество станций и ограничение на абсолютную величину их координат.
На каждый запуск зонда-разведчика вводится полученная им информация — два целых числа l и r, разделенных пробелом, — количество станций-ретрансляторов слева и справа от траектории его движения соответственно.
Для запуска зонда выведите строку «? x1 y1 x2 y2», где (x1, y1) и (x2, y2) — две точки с целочисленными координатами, лежащие на прямой, по которой должен лететь зонд. Зонд будет лететь в направлении от первой точки ко второй. Точки не должны совпадать. Координаты точек не должны превосходить 5C по модулю.
Как только вы найдете ответ, выведите строку «Ready!», и в следующих N строках выведите координаты станций в любом порядке. После этого ваша программа должна завершиться.
4 5
0 4
0 3
0 3
0 2
1 1
3 1
3 0
3 0
? -1 3 1 3
? -1 2 1 2
? -1 1 0 2
? -1 0 0 2
? 0 0 0 2
? 1 0 1 2
? 2 0 2 2
? 3 0 1 2
Ready!
0 -1
2 1
0 2
-1 0
В точности соблюдайте формат выходных данных. После вывода каждой строки сбрасывайте буфер вывода — для этого используйте flush(output) на языке Паскаль или Delphi, fflush(stdout) или cout.flush() в C/C++, sys.stdout.flush() на языке Python, System.out.flush() на языке Java.
Программа не должна делать более 105 запросов запуска зонда. При превышении этого количества, тест будет не пройден с вердиктом «Wrong Answer».
Тесты к этой задаче состоят из четырех групп.
- Тест 1. Тест из условия, оцениваемый в ноль баллов.
- Тесты 2–11. В тестах этой группы N = 3, C ≤ 10. Эта группа оценивается в 30 баллов.
- Тесты 12–24. В тестах этой группы N ≤ 50, C ≤ 100. Эта группа оценивается в 30 баллов. Решение будет тестироваться на тестах этой группы только в случае прохождения всех тестов из первой группы.
- В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов. Решение будет тестироваться на тестах этой группы только в случае прохождения
всех тестов из первой и второй группы.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы.
4 5 -1 0 0 -1 2 1 0 2
28
В городе, являющемся одним из ведущих Российских образовательных центров, решили построить пивную. Естественно, что ректоры находящихся в городе ВУЗов потребовали, чтобы пивная была максимально удалена от каждого из ВУЗов. Помогите директору будущей пивной выбрать оптимальное место для строительства. Граница города представляет собой выпуклый многоугольник. Положение ВУЗов задается координатами точек внутри этого многоугольника. Пивную нужно построить так, чтобы расстояние от нее до ближайшего вуза было максимально. Пивную можно строить как внутри города, так и на его границе.
В первой строке потока ввода задается число \(3 \le N \le 10\) – количество вершин многоугольника, являющегося границей города. В следующей строке – \(2*N\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами вершин многоугольника, перечисленными в порядке обхода границы города против часовой стрелки. Никакие две вершины многоугольника не совпадают, никакие три не лежат на одной прямой. В третьей строке потока ввода находится число \(1 \le M \le 100\) – количество ВУЗов в городе. В следующей строке – \(2 * M\) вещественных чисел по модулю не превосходящих 1000, являющихся координатами каждого из ВУЗов(никакие два ВУЗа не расположены в одной точке).
В первую строку выходного потока вывести минимальное расстояние от планируемого места строительства пивной до ближайшего к ней ВУЗа. Во второй строке вывести через пробел координаты места, оптимального для строительства пивной. Результаты выводить с двумя цифрами после точки.
Все вещественные числа задаются не более чем с двумя значащими цифрами после точки.
3 0 0 4 1 0 3 1 1 1
3.00 4.00 1.00