Вы наверняка слышали легенду о Короле Артуре и Рыцарях Круглого Стола. Практически все версии этой истории указывают на то, что круглость Круглого Стола тесно связана с верой Артура в равенство среди рыцарей. Это ложь! На самом деле выбор Артура касательно формы стола вызван его детской травмой.
В реальности Артур был принужден убирать и мыть квадратные столы с юного возраста после того как на них играли в бирюльки. После соревнований по этой игре обычно на столе остается множество палочек, не касающихся друг друга. В духе соревнования, организаторы установили свод строгих правил для уборщиков. Точнее, палочки со стола должны быть убраны одна за другой путем их сдвига к ближайшему к уборщику краю стола. Они не должны вращаться и касаться других палочек в процессе перемещения.
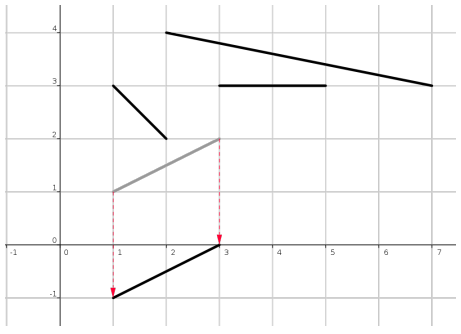
В этой задаче представим стол на координатной плоскости как квадрат с противоположными вершинами в точках (0, 0) и (10000, 10000), где палочкам соответствуют прямые отрезки, лежащие внутри квадрата. Предположим, что Артур сидит у края стола, прилежащего к оси X. Тогда уборка палочек со стола сводится к передвижению их к оси X, покуда они не упадут со стола. Ваша задача - определить порядок уборки палочек со стола, который соответствует условиям из предыдущего абзаца.
Первая строка содержит единственное целое число N ( 1 ≤ N ≤ 5000 ) - количество палочек на столе. Каждая из следующих N строк содержит 4 целых числа x 1 , y 1 , x 2 , y 2 ( 0 ≤ x 1 , y 1 , x 2 , y 2 ≤ 10000 ), обозначающих крайние точки палочек.
В единственной строке выведите N целых чисел - номера палочек в том порядке, в котором они должны быть убраны со стола. Если существует несколько решений, выведите любое из них.
4 1 3 2 2 1 1 3 2 2 4 7 3 3 3 5 3
2 4 1 3
4 0 0 1 1 1 2 0 3 2 2 3 3 4 0 3 1
4 3 1 2
3 4 6 5 5 2 1 15 1 3 2 8 7
2 3 1
Хранители в опасности, и Доктор Манхэттен со своим другом Дэниелом Драйбергом должны срочно их предупредить. Всего в команде хранителей n человек, i -й из которых находится в точке плоскости с координатами ( x i , y i ) .
Как всем известно, доктор Манхэттен вычисляет расстояние между двумя хранителями
i
и
j
по формуле
|
x
i
-
x
j
| + |
y
i
-
y
j
|
. Дэниел, как обычный человек, считает, что расстояние равно
 .
.
Сейчас успех операции зависит от того, сколько существует пар ( i , j ) ( 1 ≤ i < j ≤ n ), таких что расстояние между хранителем i и хранителем j , вычисленное Доктором Манхэттеном, равняется расстоянию между ними, вычисленному Дэниелом. Вычислить эту величину попросили именно вас.
В первой строке входных данных записано число n ( 1 ≤ n ≤ 200 000 ) — количество хранителей.
В каждой из следующих n строк записаны два целых числа x i и y i ( | x i |, | y i | ≤ 10 9 ).
Выведите количество пар хранителей, таких что расстояние между ними, вычисленное доктором Манхэттеном, равно расстоянию, вычисленному Дэниелом.
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов предыдущих групп.

В первом примере расстояние между хранителем
1
и хранителем
2
равняется
|1 - 7| + |1 - 5| = 10
в понимании Доктора Манхэттена и
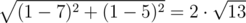 в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
в понимании Дэниела. Для пар
(1, 1)
,
(1, 5)
и
(7, 5)
,
(1, 5)
расстояния, вычисленные Доктором Манхэттеном и Дэниелом, совпадают.
3 1 1 7 5 1 5
2
6 0 0 0 1 0 2 -1 1 0 1 1 1
11
Организаторы CEOI 2011 собираются устроить вечеринку с кучей воздушных шариков. Всего будет \(n\) шариков (они все имеют форму идеального шара), и они будут лежать на одной линии на полу.
Шарики ещё не надуты, и каждый из них изначально имеет нулевой радиус. Ещё, \(i\)-й шар прикреплён к полу в позиции \(x_i\). Они будут надуваться последовательно, слева направо. Когда какой-то шарик надувается, его радиус непрерывно увеличивается, пока не достигнет верхней границы своего размера, \(r_i\), либо же не каснётся одного из уже надутых.
 Картинка 1: Шары из примера, после надувания.
Картинка 1: Шары из примера, после надувания.
Организваторы хотели бы оценить, сколько воздуха понадобится для надувания. Найдите, пожалуйста, итоговый радиус каждого шара.
В первой строке входных данных содержится целое число \(n\) (\(1\le n\le 200 000\)) – количество шаров.
Следующие \(n\) описывают шары. \(i\)-я из них содержит два целых числа \(x_i\) и \(r_i\) (\(0\le x_i\le 10^9\)), \(1\le r_i\le 10^9\)). Последовательность \(x_i\) строго возрастает.
Выведите \(n\) строк, в \(i\)-й строке должно быть единственное целое число – радиус \(i\)-го шара после надувания. Ваш ответ будет считаться верным, если он отличается от правильного не больше, чем на 0.001 в каждом числе.
1. (40 баллов) \(n\le 2000\).
2. (60 баллов) \(n\le 200000\).
3 0 9 8 1 13 7
9.000 1.000 4.694
Теперь вас назначили управляющим одной телекоммуникационной компании. Вы отвечаете за обеспечение маленького городка контентом. Каждый дом задается его координатами на плоскости. Известно, что никакие три дома не лежат на одной прямой, а никакие четыре на одной окружности. Вы решили поставить одну антенну так, чтобы сигнал от нее был доступен домам в определенным радиусе, т.е. область, в которой доступен контент является кругом. Вы еще не очень разобрались в политике вашей компании, поэтому решили сделать не слишком сложный выбор данной области: вы просто выбираете 3 случайных дома и строите круг так, чтобы эти три дома были на его границе (вы ходили на геометрию в 7 классе и вам известно, что так всегда можно сделать). Теперь вам интересно, сколько в среднем домов будут иметь доступ к контенту. Выведите ответ с точностью до 4 знаков после запятой.
Первая строка входных данных содержит одно число \(3 \le n \le 1500\) - кол-во домов. Каждая из следующих \(n\) строк содержит два целых числа \(-10^6 \le x_i, y_i \le 10^6\) - координаты \(i\)-го дома.
Выведите одно число - ответ на задачу с точностью до 4 знаков после запятой.
Подзадача 1(40 баллов) \(1 \le n \le 100\)
Подзадача 2(30 баллов) \(1 \le n \le 500\)
Подзадача 3(30 баллов) \(1 \le n \le 1500\)
4 0 2 4 4 0 0 2 0
3.500000