Темы --> Информатика --> Алгоритмы --> Вычислительная геометрия --> Многоугольники. Выпуклые оболочки
---> 38 задач <---
Источники
    Личные олимпиады(938 задач)
    Командные олимпиады(684 задач)
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
#452
Принадлежность точки произвольному многоугольнику
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Задан многоугольник и точка. Нужно определить, лежит ли точка внутри этого многоугольника. В этой задаче многоугольник невыпуклый.

Входные данные

Сначала вводится число N (3<=N<=100). Далее идут N пар вещественных чисел, задающих координаты вершин многоугольника. Последние два вещественных числа задают координаты точки.

Выходные данные

Выведите сообщение YES, если точка лежит внутри многоугольника, или NO, если нет. Гарантируется, что точка не лежит на границе многоугольника.

Примеры
Входные данные
3
0 0
1 0
0 1
10 10
Выходные данные
NO
#453
Покрыть точки кругом
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Даны N точек. Требуется построить круг минимального радиуса такой, чтобы этот круг целиком покрывал все точки (допустимо, чтобы некоторые точки лежали на границе круга).

Входные данные

Сначала вводится  число N - количество точек, 3<=N<=100000. Далее идут N пар чисел, задающих координаты точек.  Координаты - вещественные числа.

Выходные данные

Выведите три числа - координаты центра и радиус искомого круга. Если решений несколько, выведите любое из них.

Примеры
Входные данные
4
0 0 
6 0
6 8
0 8
Выходные данные
 3.00000000000000E+0000  4.00000000000000E+0000  5.00000000000000E+0000
#455
Торт для жюри
  

K членов Жюри Десятой Всероссийской олимпиады школьников по информатике решили отметить столь круглую годовщину в одном из лучших ресторанов на Невском проспекте. На десерт вниманию Жюри предложили торт, имеющий форму прямоугольной призмы с выпуклым N-угольником в основании. Жюри вооружается десертными ножами и собирается справедливо разделить торт на K частей равного объема. Ножами можно проводить прямые вертикальные разрезы от одной границы торта до другой; различные разрезы могут иметь общие точки лишь в своих концевых вершинах.

Напишите программу, помогающую членам Жюри построить требуемые K-1 разрезов.

Входные данные

В первой строке входных данных содержатся два целых числа K и N (1 <= K, N <= 50). Далее следуют N пар вещественных чисел - координаты последовательно расположенных вершин N-угольника.

Выходные данные

Каждый из K-1 разрезов в выходных данных должен быть представлен четверкой вещественных чисел с не менее чем 10 знаками после запятой - координатами концов соответствующего разреза. Все числа должны быть разделены пробелами и/или символами перевода строки.

Примеры
Входные данные
2 3
1 0
0 0
0 1
Выходные данные
 1.0000000000E+00  0.0000000000E+00  0.0000000000E+00  5.0000000000E-01
#456
Целые точки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).

Входные данные

В первой строке содержится N (3≤N≤1000) - число вершин многоугольника. В последующих N строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке. Xi и Yi - целые числа, по модулю не превосходящие 1000000.

Выходные данные

Выведите одно число - искомое количество точек.

Примеры
Входные данные
4
1 1
1 2
2 2
2 1
Выходные данные
0
#458
Разрезанный прямоугольник
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.

1

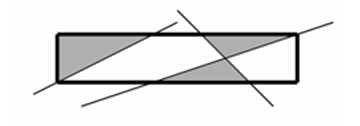
Рисунок, соответствующий 1-му примеру входных и выходных данных

Входные данные

Сначала вводятся два положительных числа X, Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.

Далее записано целое число N - количество разрезов (1≤N≤200). Далее описываются сами разрезы. Все разрезы делались вдоль  прямых. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).

Все вводимые числа  (кроме N) вещественные, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.

Выходные данные

Выведите одно целое число - количество частей исходного прямоугольника, имеющих треугольную форму.

Примеры
Входные данные
5.00 1.00
3
1.00 -2.00 0.00
1.00 -3.00 -2.00
1.00 1.00 -4.00
Выходные данные
3
Входные данные
4.00 2.00
2
1.00 -2.00 0.00
1.00 2.00 -4.00
Выходные данные
4
Страница: << 1 2 3 4 5 6 7 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест