Петя и его друг Андрейка только что познакомились с китайской мифологией. Особенно им понравились драконы. Поэтому мальчики решили сделать своих драконов из проволоки. Андрейка взял белую проволоку и согнул из неё дракона Лун-Инь: этот дракон спал, свернувшись клубком на столе. Тогда Петя взял чёрную проволоку и согнул дракона Лун-Ян. Этот дракон ничем не походил на Андрейкиного Лун-Иня. Его тело состояло из отрезков прямых, а когда он спал, то сворачивался в виде плоской замкнутой несамопересекающейся ломаной. Более того, Лун-Ян не ложился плашмя на стол для сна, а вставал перпендикулярно поверхности. Удержать равновесие дракон может только тогда, когда существуют две его различные точки, касающиеся стола, такие что центр масс дракона находится строго между ними.

Вам требуется узнать, сколько было устойчивых положений у дракона, в которых он мог сохранять равновесие во время сна, если известно, что форма ломаной в виде которой дракон спит всегда одна и та же.

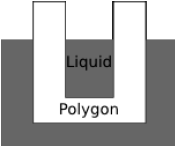
Многоугольник топят в жидкости, опуская его из воздуха с постоянной скоростью v метров в минуту. Жидкость разъедает многоугольник со всех сторон с постоянной скоростью c метров в минуту. Для точки (\(x\), \(y\)) внутри многоугольника, опускающейся вместе с ним, выясните, в какой момент разъедающая жидкость доберётся до этой точки.

Граница между воздухом и жидкостью проходит по прямой \(y\)=0. Жидкость разъедает многоугольник как двумерную фигуру. Многоугольник не поворачивается при опускании в жидкость, и в момент времени 0 он не касается жидкости.

В отличие от многоугольника, который считается двумерным, жидкость существует в трёх измерениях. Поэтому она проникает внутрь «дыр» в многоугольнике. Например, если многоугольник имеет форму «чашки», жидкость проникает «внутрь», как показано на рисунке.

На плоскости даны \(N\) точек. Вам требуется построить выпуклую оболочку данного множества точек. Если \(N\) нечетно, то оболочку нужно выводить в порядке обхода по часовой стрелке, иначе — против часовой стрелки.

Миротворцы ООН в одной из горячих точек планеты обезвреживали минное поле следующим образом. Имея карту, на которой каждая мина задана своими декартовыми координатами, они, обратив внимание на то, что никакие 3 мины не лежат на одной прямой, протянули специальный шнур от мины к мине так, чтобы он образовал выпуклый многоугольник минимального периметра, при этом все остальные мины оказались внутри многоугольника. Обезвредив соединенные мины, они вновь протянули шнур по тому же принципу, и опять обезвредили соединенные шнуром мины. Так продолжалось до тех пор, пока очередной шнур оказалось невозможным протянуть, руководствуясь изложенными правилами. Сколько мин осталось обезвредить и сколько раз саперам приходилось протягивать шнур?

Лесопильный комбинат выполняет заказ на распил брусьев для строительства детского городка. Все готовые брусья должны иметь форму треугольных призм, основаниями которых являются равнобедренные треугольники. Для изготовления брусьев закуплены заготовки в виде половинок продольно распиленных бревен. Заготовки не являются идеальными половинками цилиндров, поэтому при изготовлении бруса необходимо учитывать форму заготовок. Комбинат заинтересован в изготовлении бруса с наибольшей возможной площадью поперечного сечения.

Для каждой заготовки измеряется несколько сечений. Каждое из них задано в виде ломаной, представленной координатами ее вершин (\(x_0, y_0\)), (\(x_1, y_1\)), ..., (\(x_N, y_N\)) в порядке их следования. Координаты вершин ломанной удовлетворяют следующим условиям:

\(x_0 < x_1 < x_2 < \dots < x_N\);

\(x_i = 0\) для некоторого \(0 < i < N\);

\(y_0 = y_N = 0\);

\(y_0 = y_N = 0\);

для всех \(i\) от 1 до (\(N – 1\)) выполнено условие \(y_i > 0\).

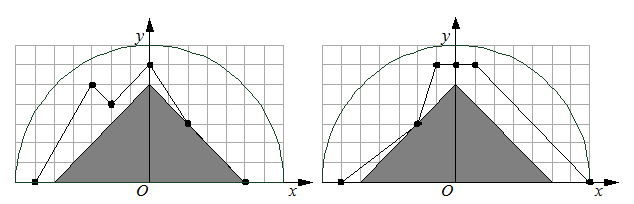
С учетом описанных требований необходимо найти максимально возможную площадь равнобедренного треугольника, удовлетворяющего следующим условиям:

основание треугольника лежит на оси абсцисс;

основание симметрично относительно начала координат;

треугольник полностью лежит внутри каждого из измеренных сечений заготовки.

Требуется написать программу, которая по заданным сечениям заготовки вычислит максимально возможную площадь искомого равнобедренного треугольника.