Польская армия движется из Костромы в деревню Домнино. Два гетмана Стефан и Константин руководят армией. Стефан изучил карту дорог Костромской губернии и каждую ночь он ведет армию от одной деревни к некоторой другой по некоторой дороге. Константин достал карту секретных троп между деревнями и каждый день он возглавляет марш-бросок армии вдоль одной из этих троп. Каждый гетман перед маршем спрашивает дорогу у Ивана Сусанина. Таким образом, в первый день Стефан возглавляет поход, на следующий день - Константин, потом - снова Стефан и т.д.
Длина каждой дороги указана на карте Стефана. Поэтому Стефан знает минимальное расстояние от каждой деревни до Домнино, аналогично Константин знает минимальное расстояние до Домнино по своей карте. Иван Сусанин каждый раз выбирает дорогу для Стефана или тропу для Константина так, что минимальное расстояние между войском и Домнино по соответствующей карте все время строго убывает.

Помогите Ивану найти самый длинный путь в Домнино, удовлетворяющий этим условиям. Гарантируется, что Домнино достижимо из каждой деревни.
Первая строка входа содержит три целых числа N, S и T – количество деревень, номер начальной деревни и номер деревни Домнино (2 ≤ N ≤ 1000, 1 ≤ s, t ≤ N). Начальная точка не совпадает с Домнино.
Далее идут описание карты Стефана и карты Константина
Первая строка описания карты содержит число M – количество дорог или троп соответственно (1 ≤ M ≤ 100000). Каждая из следующих М строк содержит 3 целых числа a, b и l – описывающих дорогу/тропу между пунктами a и b с указанием длины l (1 ≤ a, b ≤ N; 1 ≤ l ≤ 106).
Выведите общую длину пути (вдоль дорог и троп), который Сусанин заставит пройти польскую армию. Если он может заставить армию ходить вечно, так и не достигая Домнино, то выведите -1.
5 1 5 5 1 2 2 1 4 2 2 3 1 3 4 1 5 3 1 4 1 2 2 2 4 2 2 3 1 2 5 2
-1
3 1 3 4 1 2 10 2 3 10 1 3 20 2 3 30 4 2 1 10 1 3 10 1 1 10 2 3 10
20
В селе Максоярославке коровы обычно пасутся на лужайках, соединенных дорожками, на каждой лужайке пасется хотя бы одна корова. При этом для каждой пары лужаек есть ровно один способ пройти от одной лужайки до другой. По каждой дорожке можно двигаться в обоих направлениях. Считается, что все дорожки имеют одинаковую длину.
Главный фермер села хочет построить на лужайках \(k\) коровников для своих коров. Ясно, что каждая корова вечером будет возвращаться именно в тот
коровник, который ближе к ее лужайке (если расстояние до коровников
одинаково, то в любой из них). Поэтому возникает задача определения
такого расположения коровников, при котором наибольшее из расстояний,
проходимых коровами, было бы минимально.
В первой строке входного файла содержатся два числа \(n\) и \(k\) (\(2 \le n \le 50\;000\), \(1 \le k \le n\)) --- количество лужаек и планируемое число коровников, соответственно. Следующие \(n - 1\) строк содержат описания дорожек. Каждая дорожка задается парой целых положительных чисел (\(a, \, b\)), где \(a\) и \(b\) --- номера лужаек, которые соединяет данная дорожка. Лужайки нумеруются с единицы.
В первой строке входного файла выведите \(l\) --- максимальное количество дорожек, по которым придется пройти корове, чтобы попасть в коровник. Во второй строке выведите \(k\) различных целых чисел --- номера лужаек, на которых следует построить коровники. Если оптимальных решений несколько, разрешается вывести любое из них.
7 2 5 4 4 3 1 3 2 3 4 6 6 7
2 1 4
Петя работает в межгалактическом агентстве путешествий. Он часто получает запросы на поиск пути между двумя планетами по доступным межпланетным дорогам. Петя уже сделал по этому поводу целый ряд наблюдений, и сейчас его интересует следующее. Для каждой планеты \(А\) он хочет знать количество пар планет \(В\) и \(С\), таких что любой путь от планеты \(В\) к планете \(С\) проходит через планету \(А\).
Первая строка входного файла содержит два числа \(2 \leq N \leq 20000\) и \(1 \leq M \leq 200000\) – число планет и число дорог соответственно. Далее в \(M\) строках следуют описания дорог. По дорогам можно двигаться в обе стороны. Каждая дорога описывается номерами планет, которые она соединяет. Гарантируется, что от любой планеты можно добраться до любой другой.
В выходной файл выведите \(N\) чисел – для каждой планеты \(А\) выведите количество пар различных планет, таких что любой путь от одной до другой содержит \(А\).
7 9 1 2 1 3 1 4 1 5 1 6 1 7 2 3 4 5 6 7
18 6 6 6 6 6 6
Рассмотрим разновидность двоичного дерева, которую мы назовем логическим деревом. В этом дереве каждый уровень полностью заполнен, за исключением, возможно, последнего (самого глубокого) уровня. При этом все вершины последнего уровня находятся максимально слева. Дополнительно, каждая вершина дерева имеет ноль или двоих детей.
Каждая вершина дерева имеет связанное с ней логическое значение (1 или 0). Кроме этого, каждая внутренняя вершина имеет связанную с ней логическую операцию („И“ или „ИЛИ“). Значение вершины с операцией „И“ — это логическое „И“ значений её детей. Аналогично, значение вершины с операцией „ИЛИ“ — это логическое „ИЛИ“ значений её детей. Значения всех листьев задаются во входном файле, поэтому значения всех вершин дерева могут быть найдены.
Наибольший интерес для нас представляет корень дерева. Мы хотим, чтобы он имел заданное логическое значение \(v\), которое может отличаться от текущего. К счастью, мы можем изменять логические операции некоторых внутренних вершин (заменить „И“ на „ИЛИ“ и наоборот).
Дано описание логического дерева и набор вершин, операции в которых могут быть изменены. Найдите наименьшее количество вершин, которые следует изменить, чтобы корень дерева принял заданное значение \(v\). Если это невозможно, то выведите строку «IMPOSSIBLE» (без кавычек).
В первой строке входного файла находятся два числа \(n\) и \(v\) (\(1 \le n \le 10\,000, 0 \le v \le 1\)) — количество вершин в дереве и требуемое значение в корне соответственно. Поскольку все вершины имеют ноль или двоих детей, то \(n\) нечётно. Следующие \(n\) строк описывают вершины дерева. Вершины нумеруются от \(1\) до \(n\).
Первые \((n-1)/2\) строк описывают внутренние вершины. Каждая из них содержит два числа — \(g\) и \(c\), которые принимают значение либо \(0\), либо \(1\). Если \(g=1\), то вершина представляет логическую операцию „И“, иначе она представляет логическую операцию „ИЛИ“. Если \(c=1\), то операция в вершине может быть изменена, иначе нет. Внутренняя вершина с номером \(i\) имеет детей \(2i\) и \(2i+1\).
Следующие \((n+1)/2\) строк описывают листья. Каждая строка содержит одно число \(0\) или \(1\) — значение листа.
В выходной файл выведите ответ на задачу.
9 1 1 0 1 1 1 1 0 0 1 0 1 0 1
1
5 0 1 1 0 0 1 1 0
IMPOSSIBLE
В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности управления страной, выполненных ведущими экономистами Триландии.
Всего в Триландии n городов, из которых некоторые пары городов соединены дорогами, и по каждой из них можно проехать в обе стороны. Время проезда по каждой дороге в одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из каждого города можно добраться в любой другой, причем это можно сделать единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.
Как показали результаты проведенных триландскими экономистами исследований, управление страной будет наиболее эффективным, если три столицы будут выбраны так, что время кратчайшего пути между каждой парой столиц составит ровно d часов. Перед проведением выборов необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам. Две тройки городов считаются различными, если в первой тройке есть хотя бы один город, которого нет во второй тройке, и наоборот.
Требуется написать программу, которая по количеству городов в Триландии и описанию дорог находит количество троек городов, которые могут быть столицами.
Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии n и требуемое время в пути между столицами d (\(3 \leq n \leq 10^5\), \(1 \leq d < n\)). Каждая из последующих (n – 1) строк содержит описание одной дороги: пару разделенных пробелом различных целых чисел \(a_i\) и \(b_i\) — номера городов, которые соединены двусторонней дорогой (\(1 \leq a_i \leq n\), \(1 \leq b_i \leq n\), \(a_i \ne b_i\)). Каждая пара городов соединена не более чем одной дорогой.
Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут быть выбраны столицами. В случае, если нужных троек городов не окажется, выходной файл должен содержать ноль.
Пояснения к тестам
В первом примере существует единственный способ выбрать три столицы: города под номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.
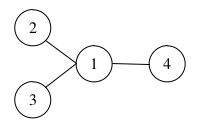
Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.
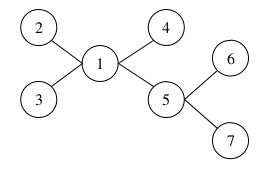
Правильные решения для тестов, в которых 3 ≤ n ≤ 50, будут оцениваться из 20 баллов.
Правильные решения для тестов, в которых 3 ≤ n ≤ 500, будут оцениваться из 40 баллов.
Правильные решения для тестов, в которых 3 ≤ n ≤ 5000, будут оцениваться из 60 баллов.
4 2 1 2 1 3 1 4
1
7 2 1 2 1 3 1 4 5 1 5 6 5 7
5