Фирма, в которой работает ваш друг, решила воспользоваться удобным моментом и купила компанию, занимающуюся пригородными автобусными пассажирскими перевозками. Таким образом, фирма вашего друга расширяет область деятельности и будет теперь обслуживать и некоторые внутриобластные автобусные маршруты.
Сейчас руководство фирмы, и в том числе ваш друг, заняты оптимизацией работы этих маршрутов. Одна из основных проблем, которые были обнаружены, состоит в том, что большинство автобусов, использующихся там, очень старые и изношенные, и поэтому часто выходят из строя. В целях улучшения ситуации было принято решение о создании сети ремонтных подстанций, которые будут располагаться в некоторых населённых пунктах области и обслуживать другие близлежащие населённые пункты.
Система дорог в области устроена следующим простым образом. Есть \(N\) населённых пунктов, некоторые из которых соединены дорогами. Между каждой парой пунктов существует не более одной дороги, и более того, для каждой пары населённых пунктов есть ровно один способ добраться из одного в другой (возможно, через промежуточные посёлки).
В каждом населённом пункте можно разместить ремонтную подстанцию. В принципе, фирма может размещать как крупные подстанции, которые даже в одиночку смогут обслуживать всю область, но при этом будут требовать больших расходов на содержание, так и небольшие станции, которые будут обслуживать лишь прилегающие населённые пункты, но при этом будут обходиться намного дешевле. Фирма уже определила, что каждую подстанцию можно характеризовать параметром “мощность”, которая может принимать значения, являющиеся целыми положительными числами (равна нулю мощность быть не может). Подстанция с мощностью \(k\) будет обслуживать населённый пункт u, в котором она расположена, и все другие населённые пункты, до которых можно добраться из u, использовав не более k дорог (т.е. при \(k\)=1, например, подстанция обслуживает свой населённый пункт и все, которые напрямую соединены с ним дорогой). Стоимость содержания такой подстанции пропорциональна её мощности.
Теперь перед руководством фирмы и, в частности, вашим другом, стоит задача придумать схему расположения подстанций в населённых пунктах области так, чтобы, во-первых, каждый населённый пункт обслуживался хотя бы одной подстанцией, а во-вторых, суммарная мощность созданных подстанций была минимальна.
Как показывает статистика, автобусы намного реже ломаются на дорогах, чем внутри населённых пунктов, где они вынуждены часто изменять скорость, останавливаться, трогаться с места, заводить двигатель и т.д., поэтому не важно, все ли дороги обслуживаются — главное, чтобы обслуживались все населённые пункты.
В первой строке входного файла находится одно число \(N\) — количество населённых пунктов в области (1<=\(N\)<=300). Далее следуют \(N\)−1 строка, описывающая дороги. Каждая строка содержит два числа — номера населённых пунктов, которые соединяет эта дорога. Населённые пункты нумеруются от 1 до \(N\).
В первую строку выходного файла выведите одно число — оптимальную суммарную мощность подстанций. Далее выведите \(N\) чисел, описывающих какое-нибудь оптимальное решение. \(i\)-ое из этих чисел должно быть равно мощности подстанции, которую в вашем решении надо расположить в пункте \(i\), или 0, если в населённом пункте \(i\) не должна находиться подстанция.
5 1 2 1 3 1 4 1 5
1 1 0 0 0 0
Как вы знаете, Васин брат живет во Флатландии. Во Флатландии n городов, соединенных n - 1 двухсторонней дорогой. Города пронумерованы от 1 до n . Из любого города можно добраться до любого другого.
Компания «Два пути», в которой работает Васин брат, выиграла тендер на ремонт двух путей во Флатландии. Путем называется последовательность различных городов, последовательно соединенных дорогами. Пути, которые надо отремонтировать, компания может выбрать самостоятельно. Единственное условие, накладываемое тендером, они не должны пересекаться (то есть иметь общих городов).
Известно, что прибыль, которую получит компания «Два пути», равна произведению длин выбранных двух путей. Считая длину каждой дороги один, а длину пути равной количеству дорог в ней, найдите максимальную возможную прибыль.
В первой строке записано целое число n (2 ≤ n ≤ 100 000) , где n количество городов в стране. Далее в n - 1 строке записаны сами дороги. Каждая строка содержит пару номеров соединяемых дорогами a i , b i (1 ≤ a i , b i ≤ n )
Выведите максимально возможную прибыль.
4 1 2 2 3 3 4
1
7 1 2 1 3 1 4 1 5 1 6 1 7
0
6 1 2 2 3 2 4 5 4 6 4
4
Много в мире разных часовых поясов! Именно поэтому соревнования по программированию часто бывают в неудобное для некоторых людей время. Как-то раз Гриша и Егор решили поучавствовать в соревновании, которое заканчивалось очень поздно. Именно поэтому ребята решили переночевать в гостинице, чтобы не возвращаться домой поздно. Однако все не так просто. Родители Егора и Гриши очень волнуются за своих детей, поэтому они решили установить по всему городу камеры, чтобы видеть, где находятся ребята.
В городе, где живут программисты 1 ≤ n ≤ 500 000 перекрестков, соединенных n - 1 дорогой так, что между любыми двумя перекрестками существует путь по дорогам.
Родители собираются установить на перекрестках города камеры, радиус действия которых равен длине дороги. Родители будут спокойны, если смогут видеть ребят на любой дороге и на любом про перекрестке. Иными словами, для каждого перекрестка должен существовать перекресток, находящийся на расстоянии не более одной дороги, такой что на нем установлена камера и для любой дороги должна быть установлена камера хотя бы на одном конце этой дороги. Установка камер — затратное дело, поэтому для каждого перекрестка с номером i известна стоимость 1 ≤ cost i ≤ 10 9 установки камеры на нем.
Помогите родителям установить камеры надлежащим образом за минимальную стоимость.
В первой строке входного файла содержится количество перекрестков n ( 1 ≤ n ≤ 500 000 ).
В последующих n - 1 строках содержатся v i u i — перекрестки соединенные очередной дорогой.
Последняя строчка входного файла содержит n чисел сost 1 , сost 2 , ..., сost n ( 1 ≤ сost i ≤ 10 9 ) — стоимости установки камер на перекрестках.
В первой строке выведете минимальную стоимость установки ans и количество перекрестков k , в которых надо установить камеры.
Во второй строке выведите k чисел — перекрестки, в которых надо установить камеры.
Если ответов несколько, разрешается вывести любой из них.
6 1 2 2 3 1 4 4 5 4 6 228 1488 2 2 8 1
232 3 1 3 4
Мирко стал генеральным директором крупной корпорации. В компании работает N человек, пронумерованных от 1 до N , Мирко имеет номер 1 . У всех кроме Мирко есть начальник. Начальник может иметь несколько подчинённых, но не более одного своего начальника.
Когда Мирко получает задание от инвесторов, он передаёт его своему подчинённому с наименьшим номером. Этот подчинённый также передаёт его своему подчинённому с наименьшим номером, и так далее, пока задание не перейдёт несчастливому работнику без подчинённых, который должен сделать задание.
Этот работник получает 1 монету, его начальник получает 2 монеты, начальник этого начальника получает 3 и так далее. Потом тот, кто на самом деле сделал работу, осознаёт, насколько эта капиталистическая система несправедлива и увольняется с работы.
Мирко получает задания до тех пор, пока в корпорации не останется всего один сотрудник — сам Мирко. Тогда он выполняет это задание, получает 1 монету и уходит из корпорации. Ему стало интересно, сколько всего монет получил каждый бывший сотрудник. Помогите ему с этим.
Первая строка содержит одно натуральное число N ( 1 ≤ N ≤ 2·10 5 ) — число сотрудников компании. Следующая строка содержит N - 1 чисел a 2 , a 3 , ... a n ( 1 ≤ a i < i ), a i — номер начальника i -го сотрудника.
Выведите N чисел, i -е число должно означать, сколько монет получил i -й сотрудник
Программы, верно работающие при 2 ≤ N ≤ 5000 оцениваются в 50 баллов.
Пояснения к первому примеру:
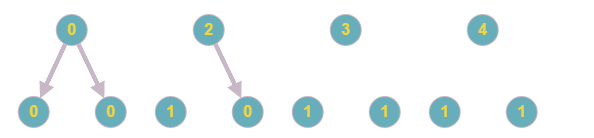
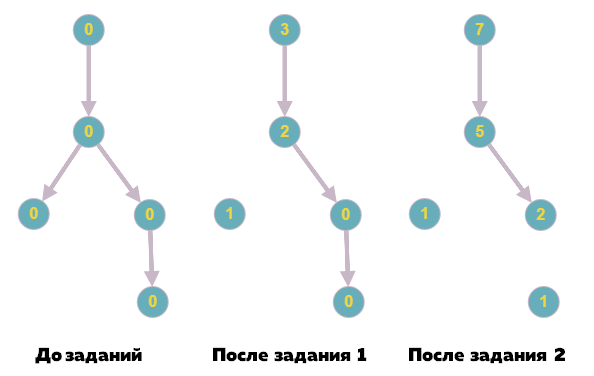
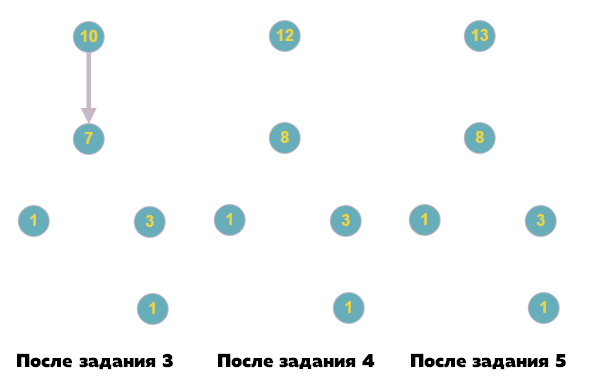
3 1 1
5 1 1
5 1 2 2 4
13 8 1 3 1
Петя увлёкся алгоритмами сжатия данных. Он уже изучил форматы gz , bz , zip и несколько других. Воодушевившись новыми знаниями, Петя собрался разработать свой формат сжатия и назвать его dis .
Петя решил сжимать таблицы. У него есть таблица, состоящая из n строк и m столбцов, заполненная целыми положительными числами. Он хочет заменить значения элементов таблицы на целые положительные числа так, чтобы отношение элементов в каждой строке и каждом столбце не изменилось. То есть, если в некоторой строке исходной таблицы a i , j < a i , k , то и в сжатой таблице a ' i , j < a ' i , k , и если a i , j = a i , k , то a ' i , j = a ' i , k . Аналогично, если в некотором столбце исходной таблицы a i , j < a p , j , то и в сжатой таблице a ' i , j < a ' p , j , и если a i , j = a p , j , то a ' i , j = a ' p , j .
Поскольку б'{о}льшие значения требуют больше места для хранения, максимальное значение элемента получившейся матрицы должно быть как можно меньше.
В теории Петя мастер, но вот писать код он не любит. Помогите ему реализовать формат сжатия dis .
В первой строке входных данных содержатся два числа
n
и
m
(
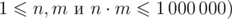 — количество строк и столбцов таблицы соответственно.
— количество строк и столбцов таблицы соответственно.
В следующих n строках содержится по m целых чисел a i , j (1 ≤ a i , j ≤ 10 9 ) — значения элементов таблицы.
Выведите сжатую таблицу: n строк, содержащих по m чисел.
Если существует несколько ответов, минимизирующих максимальное число, то разрешается вывести любой из них.
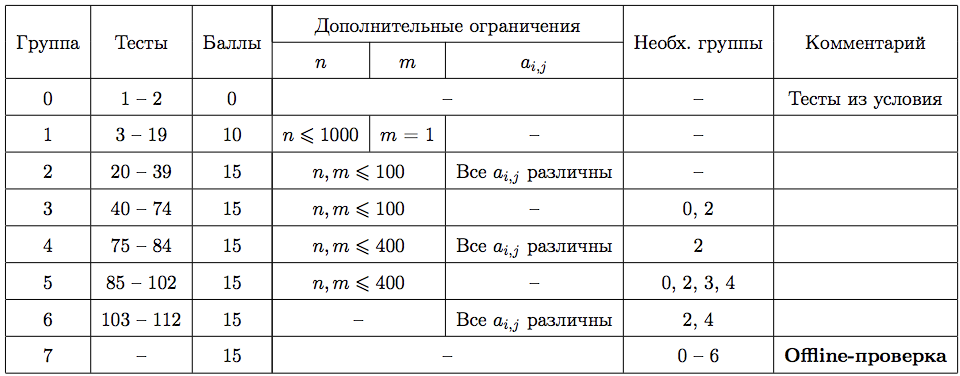
Тесты к этой задаче состоят из восьми групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп. Offline-проверка означает, что результаты тестирования вашего решения на данной группе станут доступны только после окончания соревнования.
В первом примере a 1, 2 ≠ a 2, 1 , но, поскольку они не располагаются в одной строке или в одном столбце, при сжатии их можно сделать равными.
2 2 1 2 3 4
1 2 2 3
4 3 20 10 30 50 40 30 50 60 70 90 80 70
2 1 3 5 4 3 5 6 7 9 8 7