В новой игре "Closed Loops 7" игрокам предлагается клетчатая таблица \(N\) на \(M\) клеток. Ход состоит в том, что очередной игрок рисует цикл - замкнутую линию без самопересечений, идущую только по сторонам клеток. Каждый цикл можно нарисовать только один раз за всю игру (при этом, конечно, не запрещается рисовать циклы, пересекающиеся с уже нарисованными). Игроки ходят по очереди. Выигрывает тот, кто рисует последний возможный цикл. К примеру, если \(N=2\), \(M=1\), то циклов всего три и игрок, делающий третий ход, выигрывает.
Вася позвал \(K-1\) друзей поиграть с ним. Чтобы произвести впечатление, он непременно хочет выиграть. Для этого ему нужно узнать, каким по счету игроком он должен быть, чтобы гарантированно одержать победу. Вася наслышан о ваших успехах в программировании, и за помощью он обратился именно к вам.
Даны три целых числа: \(N, M\) - размеры таблицы (\(1 \le N \le 100, 1 \le M \le 8\)) и \(K\) - количество игроков (\(1 < K \le 10^9\)).
Тесты состоят из трёх групп. В этой задаче нет off-line групп.
- Тесты 1 и 2, из условия, оцениваются в 0 баллов.
- Тесты 3--15. \(N \cdot M \le 24\). Эта группа оценивается в 40 баллов, баллы начисляются только при прохождении всех тестов группы.
- Тесты 16--42. Полные ограничения, группа оценивается в 60 баллов. Баллы начисляются только при прохождении всех тестов группы.
2 1 2
1
1 8 8064
36
Ограничение по времени – 10 секунд.
Ограничение по памяти – 64 мегабайта.
Компания Bugs начинает выпуск планки оперативной памяти Q-RAM размером 6 террабайт. Каждая планка состоит из 6 квадратных микросхем в форме прямоугольника \(3\times 2\). В результате технологического процесса, используемого в компании Bugs, получается прямоугольная область, разделенная на \(N\times M\) квадратных микросхем. После этого микросхемы тщательно проверяются и битые микросхемы помечаются черным маркером.
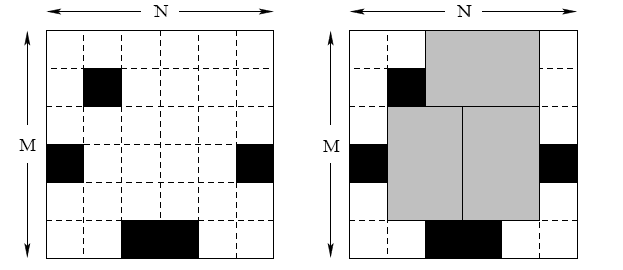
После этого, область разрезается на отдельные планки размером \(3\times 2\)(или \(2\times 3\)). Естественно, ни одна планка не должна содержать битых микросхем. Может возникнуть такая ситуация, что не все хорошие микросхемы войдут в какую-либо планку. Однако для снижения себестоимости компания хочет изготовить из произведенной области как можно больше планок.
На вход вашей программе будет даваться размер области и список битых микросхем на ней. Для этой области вам необходимо определить максимальное количество планок, которое можно вырезать из нее.
Первая строка содержит три целых числа \(N\), \(M\) и \(K\) (\(1\leq N\leq 150\), \(1 \leq M \leq 10\), \(0 \leq K \leq M\times N\)), где \(N\) – длина области, \(M\) – ее ширина, а \(K\) – количество битых микросхем. Следующие K строк содержат описание битых микросхем. Каждая из них содержит координаты битой микросхемы в виде двух целых чисел \(x\) и \(y\) (\(1 \leq x \leq N\), \(1 \leq y \leq M\)).
Для каждой области выведите максимальное количество планок, которое может быть вырезано из нее на отдельной строке.
6 6 5 1 4 4 6 2 2 3 6 6 4
3
6 5 4 3 3 6 1 6 2 6 4
4
В игре «Руммикуб» используются фишки, которые бывают четырех различных цветов, и на каждой из которых написано одно натуральное число от 1 до 13. Для каждого числа и для каждого цвета в наборе фишек есть ровно две соответствующие фишки, т.е. всего в наборе \(8\cdot 13 = 104\) фишки.
Число, написанное на фишке, будем называть ее достоинством; цвета будем обозначать латинскими буквами A, B, C и D, и каждую фишку будем обозначать, записывая сначала ее цвет, а потом — ее достоинство. Например, C12 — это фишка цвета C и достоинством 12.
Комбинацией в игре называется набор из как минимум трех фишек, удовлетворяющий любому из следующих условий:
- Достоинства всех фишек одинаковы, а цвета — попарно различны; или
- Цвета всех фишек одинаковы, а достоинства являются последовательными натуральными числами.
Например, следующие наборы фишек являются комбинациями:
-
C12,A12,B12; -
C12,A12,B12,D12; -
C5,C6,C7; -
A3,A4,A5,A6,A7.
При этом следующие наборы не являются комбинациями:
-
A3,B3(слишком мало фишек); -
A3,B3,C3,D3,B3(цвета повторяются); -
A3,A4,A4,A5,A6(достоинства повторяются); -
A3,A4,A6,A7,A8(число 5 пропущено).
Одна из основных задач в руммикубе состоит в том, чтобы данный набор фишек распределить на комбинации так, чтобы каждая фишка входила ровно в одну комбинацию. Напишите программу, которая будет это делать.
В первой строке входного файла находится одно натуральное число \(K\) — количество фишек. Далее следуют \(K\) строк, на каждой из которых находится описание одной фишки — цвет и достоинство.
Гарантируется, что эти фишки являются корректным подмножеством фишек из некоторого комплекта для игры в руммикуб; т.е. гарантируется, что каждый цвет — это латинская заглавная буква от A до D, что каждое достоинство — это натуральное число, не превосходящее 13, и что для для каждой пары (цвет, достоинство) в наборе есть не более двух таких фишек.
Если данный набор фишек можно разбить на комбинации так, чтобы каждая фишка входила ровно в одну комбинацию, то в первую строку выходного файла выведите одно число \(M\) — количество комбинаций в вашем решении. Далее выведите \(M\) строк, в \(i\)-ой из которых выведите \(i\)-ую комбинацию. А именно, сначала выведите количество фишек в комбинации, а потом сами фишки, разделенные между собой и отделенные от количества фишек пробелами. В пределах каждой комбинации фишки можете выводить в произвольном порядке; комбинации также можете выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Если решений нет, то выведите в выходной файл одно число -1.
3 A2 A3 A5
-1
3 A2 A4 A3
1 3 A2 A4 A3
7 A12 A13 A13 B13 C13 D13 A11
2 3 A11 A12 A13 4 A13 B13 C13 D13
В целях увеличения продаж фирма "Новый русский шоколад" приняла решение разбивать каждую плитку на дольки в форме прямоугольников 1 × 2 и уголков (квадрат 2 × 2 с вырезанной угловой клеткой), а не на скучные квадратики 1 × 1. При этом долек другой формы на плитке шоколада быть не должно. Через некоторое время узор на плитке будет меняться на другой (но по-прежнему состоящий только из прямоугольников 1 × 2 и уголков), через некоторое время – еще на другой и так далее. Директору фирмы "Новый русский шоколад" захотелось узнать, а сколько всего существует способов разбить плитку шоколада на такие дольки? Помогите ему найти ответ.
В одной строке вводятся два натуральных числа n и m – ширина и длина плитки (1 ≤ n, m ≤ 9).
Выведите одно целое число – количество способов разбить плитку шоколада размером n × m на прямоугольники 1 × 2 и уголки (и прямоугольник и уголок можно поворачивать, долек другой формы на плитке быть не должно).
2 3
5
3 3
8
С целью упрощения ЕГЭ по литературе, было решено оставить в нем вопросы только с ответами «да» или «нет». Бланк ответов представляет клетчатое поле из N строк и M столбцов, в котором каждая клеточка соответствует своему вопросу. Ученику необходимо один раз перечеркнуть по диагонали те клеточки, которые, по его мнению, соответствуют вопросам с ответом «нет» (перечеркивать можно по любой из двух диагоналей). При этом во избежание ошибок при сканировании, никакие две диагонали не должны "сливаться", то есть иметь общий конец.
Авторам варианта необходимо знать, какое наибольшее количество вопросов с ответом «нет» можно вставить в вариант, чтобы бланк с правильными ответами мог быть верно распознан компьютером.
Даны два натуральных числа - количество строк N и количество столбцов M. Количество вопросов в варианте не превосходит 100, то есть 1 ≤ N·M ≤ 100.
Выведите одно число – максимальное количество вопросов с ответом «нет», которое можно включить в вариант.
1 2
2
3 3
6