--->
39 задач
<---
Источники
ограничение по времени на тест
3.0 second;
ограничение по памяти на тест
512 megabytes
Компания « Rapid City Dynamics » знаменита её роботами-собаками, роботами-гепардами и даже человекоподобными роботами. Но большие проекты требуют больших денег, так что компания решила создать что-то простое, но популярное (и более востребованное). Так что компания разрабатывает нового робота « Rat-O-Matic », и вы, как работник « Rapid City Dynamics », принимаете участие в этом.
Робот выглядит как механическая крыса, которая может двигаться и генерировать мелодию, наступая на специальные рамки. Плоскость бесконечна во все стороны, и на ней задана декартова система координат.
Есть ровно n рамок. Каждая рамка задана тремя числами: x , y и r . Она задаёт территорию, ограниченую между двух квадратов со сторонами параллельным осям координат и центрами в точке ( x , y ): радиус первого квадрата r , а второго — 2· r . Радиус квадрата — это расстояние между его центром и стороной. Ко всему прочему, каждой рамке соответствует своя нота. Сейчас есть только 3 возможных ноты, обозначим их как « r », « a » и « t ».
Гарантируется, что никакие две рамки не касаются и не пересекаются.
Вы можете взаимодействовать с роботом, вбивая номер рамки на специальной клавиатуре (рамки пронумерованы начиная с 1 ). Изначально, крыса находится снаружи всех рамок. Благодаря патентованной системе навигации, робот выбирает путь до рамки, который пересекает минимальное количество рамок. Когда крыса наступает на рамку в первый раз, соответствующая нота добавляется в мелодию. Робот останавливается после того, как наступит на нужную рамку.
Известно, что людям нравятся похожие мелодии. В вашей базе данных имеются m мелодий. Каждая мелодия задаётся строкой из символов, которая задаёт ноты. Мелодия, сгенерированная крысой, содержится в мелодии из базы данных, если она содержится в ней в качестве подстроки. Популярность сгенерированной мелодии - это число мелодий в базе данных, которые содержат её. Одинаковые мелодии из базы данных должны быть учтены несколько раз.
В попытке создания самого классного расположения рамок, вы совершили q экспериментов. Эксперименты бывают трёх типов:
- Выключить рамку x . Гарантируется, что рамка была включена до этой операции. Выключенные рамки не влияют на мелодию крысы. Вначале все рамки включены.
- Включить рамку x . Гарантируется, что рамка была выключена до этой операции.
- Посчитать популярность мелодии, сгенерированной роботом при движении от точки с координатами ( 10 9 , 10 9 ) до рамки x . Гарантируется, что рамка x является включённой.
Твоя задача — провести эти эксперименты, используя только свой компьютер!
Входные данные
В первой строке содержится натуральное число n — количество рамок ( 1 ≤ n ≤ 2·10 5 ).
В следующих
n
строках описаны рамки,
i
-я из них содержит три натуральных числа
x
i
,
y
i
,
r
i
и символ
c
i
, разделённые пробелами (
- 10
8
≤
x
i
,
y
i
≤ 10
8
,
1 ≤
r
i
≤ 10
8
, и
c
i
{«
r
», «
a
», «
t
»} — координаты центра рамки, радиус внутреннего квадрата и её нота, соответственно.
Следующая строка содержит натуральное число m — количество мелодий в базе ( 1 ≤ m ≤ 2·10 5 ).
Следующие m строк содержат непустые строки из букв « r », « a » или « t », которые задают мелодии. Суммарная длина всех строк не превосходит 2·10 5 .
Следующая строка содержит натуральное число q — количество экспериментов ( 1 ≤ q ≤ 2·10 5 ).
Следующие q строк описывают эксперименты, j -я из них содержит символ t j (« - », « + » или « ? ») и натуральное число x j отделённое пробелом. Символ задаёт тип эксперимента (« - » — 1, « + » — 2 и « ? » — 3), а число обозначает номер рамки.
Гарантируется, что есть хотя бы один эксперимент третьего типа.
Выходные данные
Для каждого эксперимента третьего типа, выведите одно число — популярность получившейся мелодии.
Группы тестов (Все группы независимы)
10 баллов — (1 ≤ n, m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 2-6) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 7-9) .
10 баллов — ( 1 ≤ n, q ≤ 100, 1 ≤ m ≤ 200 000 , суммарная длина строк не превосходит 200 000, тесты 10-13) .
10 баллов — ( 1 ≤ n ≤ 4 000, 1 ≤ m ≤ 200 000, 1 ≤ q ≤ 100, суммарная длина строк не превосходит 200 000, тесты 14-16) .
10 баллов — ( 1 ≤ n ≤ 200 000, 1 ≤ m, q ≤ 100, суммарная длина строк не превосходит 100, тесты 17-19) .
15 баллов — ( 1 ≤ n, q ≤ 200 000, 1 ≤ m ≤ 100, суммарная длина строк не превосходит 100, тесты 20-23) .
35 баллов — полные ограничения, тесты 24-57.
Примеры
Входные данные
3 3 3 4 r 2 4 1 a 14 4 1 t 3 rat rara aaa 6 ? 3 ? 2 - 1 ? 2 + 1 ? 2
Выходные данные
1 2 3 2
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes
В один прекрасный день маленький Дональд решил вымыть N своих чистых белых простыней. После мытья он положил их на землю во дворе, чтобы их высушить. Дональд помещал простыни так, чтобы никакие две простыни не касались ни сторонами, ни углами, и чтобы их стороны не пересекалась, но возможно, что он разместил меньшие простыни поверх более крупных или что простыня полностью закрывает какие-то другие простыни. Сделав это, Дональд лег спать.
Друг Дональда Ким как-то узнал о том, что Дональд сушит простыни и решил пообщаться с ним. Он нашел пейнтбольный пистолет своего отца на чердаке. Наряду с пистолетом у него было несколько пейнтбольных мячей, каждый из них имел свой цвет (не обязательно уникальный). Как только Дональд заснул, Ким вошёл во двор к Дональду и начал стрелять пр простыням из пейнтбольного пистолета. Простыни Дональда очень тонкие, поэтому, когда Ким попадает в какую-то простыню, она пропускает краску дальше, на простыню ниже (и та тоже, и так происходит, пока не закончатся простыни и краска не попадет на землю). После того, как Ким использовал все шары, он с радостью покинул двор Дональда. Дональд был очень расстроен, увидев, что случилось с его простынями. Дональд очень заинтересован в правильных данных о преступлении Кима, но он в шоке и не способен думать, поэтому просит вас сказать ему количество цветов на каждой простыне.
Мы можем представлять двор Дональда как бесконечную систему координат, а простыни - как прямоугольники, параллельные осям координат. Выстрелы Кима могут быть представлены как точки в этой системе.
Когда-то в детстве дедушка рассказал Киму, что снаряд никогда не попадает в одну воронку дважды, так что координаты всех выстрелов попарно различны.
Входные данные
Первая строка ввода содержит два числа - количество простынь N ( 1 ≤ N ≤ 80000 ), и количество шаров M ( 1 ≤ M ≤ 80 000 ).
i -я из следующих N строк содержит четыре числа: координаты нижнего левого угла A i , B i ( 1 ≤ A i , B i ≤ 10 9 ) и верхнего правого угла C i , D i , ( 1 ≤ C i , D i ≤ 10 9 ) i -й простыни.
j -я из следующих M строк содержит три числа, где X j , Y j ( 1 ≤ X j , Y j ≤ 10 9 ) - координаты j -го выстрела Кима и K j ( 1 ≤ K j ≤ 10 9 ) - цвет j -го пейнтбольного шара.
Выходные данные
i -я из N выходных строк должна содержать количество цветов на i -м листе.
Система оценки
Тесты к данной задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов необходимых групп.
Примеры
Входные данные
2 2 1 1 3 3 5 6 10 10 3 3 1 5 1 2
Выходные данные
1 0
Входные данные
3 3 1 1 7 7 2 2 6 6 3 3 5 5 4 4 1 2 6 2 4 7 3
Выходные данные
3 2 1
Входные данные
1 3 1 1 7 7 2 6 2 4 7 3 4 4 1
Выходные данные
3
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
128 megabytes
Вы когда-нибудь мечтали стать главным героем компьютерной игры? Главный герой этой истории, Бранимир, мечтает сейчас именно об этом.
Мир в мечте Бранимира состоит из N небоскребов, пронумерованных слева направо. Для i -го небоскреба, известна его высота H i и количество золотых монет G i на крыше этого небоскреба. Игра начинается с прыжка на любой из небоскребов и состоит из нескольких ходов. На каждом ходу Бранимир может прыгнуть на любой небоскрёб, находящийся справа от него, но так, чтобы высота нового небоскрёба была не меньше того небоскрёба, на котором сейчас сидит Бранимир. Оказавшись на крыше небоскреба, Бранимир собирает все золотые монеты на ней. Бранимир может закончить игру после любого количества шагов (возможно, нулевого), но он должен собрать не менее K золотых монет, чтобы перейти на следующий уровень.
Бранимир хочет узнать, сколько существует способов сыграть в эту игру так, чтобы перейти на следующий уровень. Две игры называются разными, если существует небоскреб который был посещен в одной игре, но не был посещён в другой.
Входные данные
Первая строка содержит 2 натуральных числа N и K ( 1 ≤ N ≤ 40 , 1 ≤ K ≤ 4·10 10 ) — число небоскрёбов и количество монет, которые надо набрать соответственно.
Следующие N строк содержат информацию о небоскрёбах. В i -й строке даны 2 числа H i и G i ( 1 ≤ H i , G i , ≤ 10 9 ) — высота и количество монет на i -м небоскрёбе.
Выходные данные
В единственной строке вывода выведите число возможных игр, в которых Бранимир сможет пройти на следующий уровень.
Система оценки
Решение, корректно работающее при n ≤ 20 будет оцениваться в 40 баллов.
Примеры
Входные данные
4 6 2 1 6 3 7 2 5 6
Выходные данные
3
Входные данные
2 7 4 6 3 5
Выходные данные
0
Входные данные
4 15 5 5 5 12 6 10 2 1
Выходные данные
4
#114061
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes
Вы знаете, в чём разница между отелем и мотелем? Верно, разница в количестве мух, которые там живут. Норман – владелец одного из самых популярных мотелей в Америке,но его мать хочет, чтобы он стал отелем. Именно поэтому Норман купил мухобойку ( мухобойка – инструмент для отпугивания или прихлопывания мух. Может представлять собой как пластиковое или резиновое изделие на длинной ручке, так и пучок волос или листьев). Мухобойка представляет из себя многоугольник из \(\)\(K\)\(\) рёбер.
Желая угодить своей матери, Норман встал у окна, на котором сидели \(\)\(N\)\(\) мух. Так как норманн – пацифист, он не может причинить вред другому живому существу, в том числе, мухе. Именно поэтому ему интересно количество способов ударить по окну мухобойкой, не задев ни одной мухи.
Окно представляет из собой прямоугольник с левой нижней вершиной в точке \(\)\((0, 0)\)\(\) и правой верхней – в точке \(\)\((X_p, Y_p)\)\(\). После того как Норман ударит по окну все вершины многоугольника должны лежать в точках с целыми координатами, а мухобойка должна полностью лежать внутри прямоугольника окна. Норману интересно, сколькими способами он может ударить по окну, не убив ни единой мухи.
Входные данные
Первая строка содержит три числа \(\)\(X_p, Y_p, N\)\(\) (\(\)\(1 \leq X_p, Y_p \leq 500\)\(\), \(\)\(0 \leq N \leq X_p\cdot Y_p\)\(\)) — координаты верхней правой точки окна и количество мух на окне соответственно.
Следующие \(\)\(N\)\(\) строк содержат по \(\)\(2\)\(\) целых числа \(\)\(x_i, y_i\)\(\), задавая координаты мух на окне (\(\)\(0 < x < X_p\)\(\), \(\)\(0 < y_i < Y_p\)\(\)).
В следующей строке вводится одно число \(\)\(K\)\(\) (\(\)\(3 \leq K \leq 10\,000\)\(\)) — количество вершин многоугольника мухобойки. Следующие \(\)\(K\)\(\) строк содержат по два числа \(\)\(x_j, y_j\)\(\) (\(\)\(-10^9 \leq x_j, y_j \leq 10^9\)\(\)), задавая \(\)\(j\)\(\)-ю вершину многоугольника. Вершины многоугольника заданы в порядке обхода по или против часовой стрелке.
Выходные данные
Выведите искомое число способов ударить по окну, не задев ни одной мухи.
Система оценки
Решение, правильно работающее на тестах, в которых \(\)\(1 \leq X_p, Y_p \leq 100\)\(\) будет оцениваться в \(\)\(62\)\(\) балла.
Примечание
Пояснение к третьему примеру:
Примеры
Входные данные
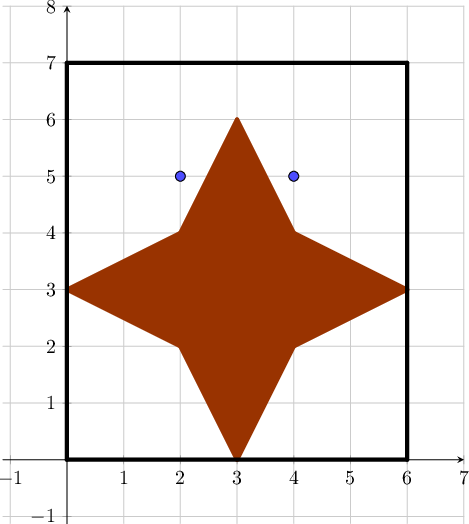
4 5 2 1 3 3 4 4 0 0 2 0 2 2 0 2
Выходные данные
4
Входные данные
5 5 3 1 4 1 3 2 2 3 4 7 6 3 7 6
Выходные данные
3
Входные данные
6 7 2 2 5 4 5 8 1 4 3 3 4 1 5 3 7 4 5 5 4 7 3 5
Выходные данные
1
Выбрано
:
|