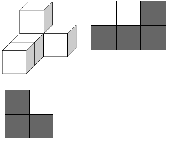
Трехмерная фигура состоит из единичных кубиков. По фигуре можно построить ее фронтальную и правую проекции. Очевидно, что по этим двум проекциям не всегда можно восстановить фигуру.
Напишите программу, которая получает на вход фронтальную и правую проекции фигуры и определяет минимальное и максимальное количество кубиков, которое можно было бы использовать для построения фигуры с заданными проекциями.
В первой строке входного файла находятся три числа N, M и К, которые задают размеры проекций (1≤N, M, K≤100). Дальше задаются две проекции: сначала фронтальная, а затем правая. Проекция задается N строками, каждая из которых состоит из чисел 0 и 1, разделенных пробелами. Для фронтальной проекции таких чисел будет M, а для правой — K. 0 означает свободную клетку проекции, 1 — заполненную.
В единственной строке выходного файла должно находиться два числа: минимальное и максимальное число кубиков, которые можно было бы использовать для построения фигуры с заданными проекциями.
2 2 3 1 0 1 1 0 0 1 1 1 1
4 7
На плоскости задано такое множество из N многоугольников, что выполняются следующие условия:
- никакие два многоугольника не имеют общих точек;
- для каждого i –го многоугольника существует Pi многоугольников, внутри которых он находится, и N-1-Pi многоугольников, которые находятся внутри его, 0 ≤Pi≤N-1.
Напишите программу, которая для каждого многоугольника выдает количество многоугольников, внутри которых он находится.
Первая строка входного файла содержит целое число N — количество многоугольников, 3≤N≤100000. Следующие N строк файла описывают N многоугольников. (i+1)–ая строка файла описывает i–ый многоугольник. Первое целое число Ci — количество вершин многоугольника, 3≤Ci≤20. Последующие Ci пар чисел — координаты вершин многоугольника в порядке его обхода. Координаты вершин — целые числа, принадлежащие диапазону от -2 000 000 000 до 2 000 000 000.
Единственная строка выходного файла должна содержать N чисел: i–ое число строки должно быть Pi — количество многоугольников, внутри которых находится i–ый многоугольник.
3 3 -2 1 8 9 12 1 3 7 5 6 3 7 4 4 4 3 7 7 9 3 1 2
0 2 1
Прямоугольное поле состоит из N строк и M столбцов. Игровая фишка за один ход может переместиться с клетки одного столбца на одну из клеток следующего столбца. Для каждой клетки поля известны номера строк клеток следующего столбца на которые фишка может сделать ход. Фишка не может пойти на клетку, которую она уже посещала раньше.
В начале игры фишку устанавливают на произвольную клетку первого столбца. После этого фишка начинает двигаться в сторону последнего столбца. Когда фишка достигает последнего столбца, ее снова устанавливают на любую клетку первого столбца, которая не была посещена раньше, и возобновляют ее движение.
Игра завершается когда фишка не может сделать ход.
Напишите программу, которая по числам N, M (1≤N≤50, 2≤M≤10), и таблице переходов между клетками определяет какое наибольшее количество раз можно провести фишку от первого до последнего столбца игрового поля.
В первой строке входного файла находятся числа N иM. Далее следует M-1 блок по N строк в каждом — описание возможных переходов для каждой клетки поля. Каждая i–ая строка j–го блока описывает возможные переходы из клетки в i–ой строке и j–ом столбце игрового поля. Первое число в строке задает количество возможных переходов из клетки, после чего следуют номера строк следующего столбца по возрастанию и без повторений.
В единственной строке выходного файла должно находиться целое число, которое соответствует искомому количеству путей. (Ответ может быть 0, если ни из одной клетки первого столбца нельзя достичь ни одной клетки последнего). Для приведенного примера входных данных фишку можно провести 3 раза, например, по таким маршрутам: (133), (244) и (422).
4 3 2 1 3 3 1 2 4 0 2 2 3 1 2 1 2 1 3 2 2 4
3