Ася Вуткина - известный футбольный комментатор. Будучи профессионалом своего
дела, Ася тщательно следит за всеми матчами всех европейских чемпионатов.
Благодаря накопленной информации, Ася может во время трансляции матча
сообщить какую-нибудь интересную статистику, например: "Индзаги
третий матч подряд забивает гол на 9-й минуте" или "Матерацци никогда не
открывает счет в матче".
Но мозг Аси не безграничен, а помнить всю историю футбола просто невозможно.
Поэтому Ася попросила вас написать программу, которая собирает статистику
матчей и умеет отвечать на некоторые запросы, касающиеся истории футбола.
Информация о матче сообщается программе в следующей форме:
"Название 1-й команды" - "Название 2-й команды" Счет 1-й команды:Счет 2-й команды
Автор 1-го забитого мяча 1-й команды Минута, на которой был забит мяч'
Автор 2-го забитого мяча 1-й команды Минута, на которой был забит мяч'
...
Автор последнего забитого мяча 1-й команды Минута, на которой был забит мяч'
Автор 1-го забитого мяча 2-й команды Минута, на которой был забит мяч'
...
Автор последнего забитого мяча 2-й команды> <Минута, на которой был забит мяч>'
Запросы к программе бывают следующих видов:
Total goals for Название команды
- количество голов, забитое данной командой за все матчи.
Mean goals per game for Название команды
- среднее количество голов, забиваемое данной командой за один матч.
Гарантирутся, что к моменту подачи такого запроса команда уже сыграла
хотя бы один матч.
Total goals by Имя игрока
- количество голов, забитое данным игроком за все матчи.
Mean goals per game by Имя игрока
- среднее количество голов, забиваемое данным игроком за один матч
его команды.
Гарантирутся, что к моменту подачи такого запроса игрок уже забил хотя бы
один гол.
Goals on minute Минута by Имя игрока
- количество голов, забитых данным игроком ровно на указанной минуте матча.
\texttt{Goals on first <\(T\)> minutes by <Имя игрока>}\\
--- количество голов, забитых данным игроком на минутах с первой по
\(T\)-ю включительно.
Goals on last \(T\) minutes by Имя игрока
- количество голов, забитых данным игроком на минутах с \((91 - T)\)-й по
90-ю включительно.
Score opens by Название команды
- сколько раз данная команда открывала счет в матче.
Score opens by Имя игрока
- сколько раз данный игрок открывал счет в матче.
Выходные данные
Для каждого запроса во входном файле выведите ответ на этот запрос в отдельной
строке. Ответы на запросы, подразумевающие нецелочисленный ответ, должны быть
верны с точностью до трех знаков после запятой.
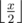 клеток до стены (
клеток до стены (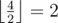 ,
, 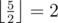 ).
).