Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Известный частный сыщик поставил чашку с чаем на специальную подогревающую подставку, питающуюся от USB-порта его компьютера, и приступил к обдумыванию очередного запутанного преступления. Через пару часов раздумий он понял, что для разгадки этого дела достаточно определить, была ли на месте преступления шахматная доска.
Недавно он получил по электронной почте фотографию места преступления. Подозрительный фрагмент (тот, на котором изображен предмет, похожий на шахматную доску) уже был скопирован в отдельный файл, но вдруг выяснилось, что, поскольку фотография была сжата с потерей качества, некоторые пиксели на ней из белых или черных стали серыми. Таким образом, определение того, является ли сфотографированный предмет шахматной доской, стало намного более сложным.
Все усложняется тем, что на фотографию могла попасть не вся шахматная доска, а лишь ее часть. Например, на приведенном рисунке на фотографию попала часть доски, у которой каждое поле имеет длину стороны, равную трем пикселям.


Помогите частному сыщику в расследовании преступления. Напишите программу, которая определит, может ли заданный фрагмент фотографии быть изображением части шахматной доски, и, если может, восстановит изображение шахматной доски до сжатия.
Шахматная доска – это квадрат, разбитый на x2 (для некоторого x) равных квадратов – полей. Стороны полей параллельны сторонам изображения. Длина стороны каждого поля шахматной доски выражается целым числом пикселей. Все пиксели, принадлежащие одному полю, покрашены в один и тот же цвет – черный или белый. При этом соседние поля (поля, имеющие общую сторону) покрашены в различные цвета.
В первой строке вводятся два целых числа: m и n – размеры фрагмента фотографии в пикселях ( 1![]() m, n
m, n![]() 250).
250).
Следующие m строк содержат по n символов каждая, j-й символ i-й строки соответствует пикселю с координатами (i, j). Символ «.» (точка) означает белый пиксель, символ «*» – черный, символ «?» – серый.
Если заданный фрагмент фотографии может быть изображением части шахматной доски, выведите слово «YES». После этого выведите m строк по n символов в каждой – изображение соответствующей части шахматной доски в том же формате, что и во входных данных, только серые пиксели должны быть заменены на белые или черные. Если решений несколько, выведите любое.
В противном случае программа должна вывести слово «NO».
4 5 *.?.? .***. .*?*. .*?*.
YES *...* .***. .***. .***.
4 5 ..?.. .***. .*?*. .*?*.
NO
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более, чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
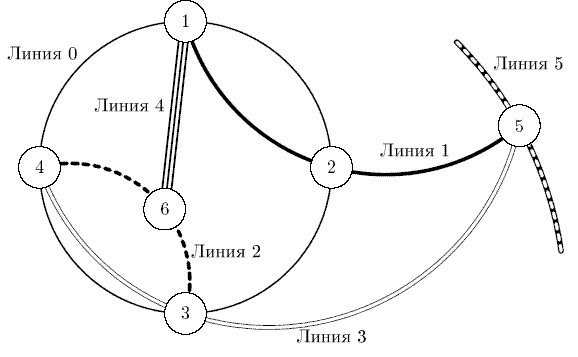
На рисунке приведена возможная схема метро, соответствующая второму примеру.
В первой строке вводится число k – количество линий метро в городе ( 1![]() k
k![]() 10). Все линии пронумерованы от 0 до k - 1, кольцевая линия имеет номер 0. Во второй строке записано число n – количество пересадочных станций. Каждая из следующих n строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
10). Все линии пронумерованы от 0 до k - 1, кольцевая линия имеет номер 0. Во второй строке записано число n – количество пересадочных станций. Каждая из следующих n строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
4 6 2 0 1 2 0 2 2 0 3 2 0 1 2 0 2 2 0 3
NO
6 6 3 0 1 4 2 0 1 3 0 2 3 3 0 2 3 3 1 3 5 2 2 4
YES
Петя нарисовал на бумаге n кружков и соединил некоторые пары кружков линиями. После этого он раскрасил каждый кружок в один из трех цветов – красный, синий или зеленый.
Теперь Петя хочет изменить их раскраску. А именно – он хочет перекрасить каждый кружок в некоторый другой цвет так, чтобы никакие два кружка одного цвета не были соединены линией. При этом он хочет обязательно перекрасить каждый кружок, а перекрашивать кружок в тот же цвет, в который он был раскрашен исходно, не разрешается.
Помогите Пете решить, в какие цвета следует перекрасить кружки, чтобы выполнялось указанное условие.
В первой строке вводятся два целых числа n и m – количество кружков и количество линий, которые нарисовал Петя, соответственно ( 1![]() n
n![]() 1 000, 0
1 000, 0![]() m
m![]() 20 000).
20 000).
Следующая строка содержит n символов из множества {'R', 'G', 'B'} – i-й из этих символов означает цвет, в который раскрашен i-й кружок ('R' – красный, 'G' – зеленый, 'B' – синий).
Далее в m строках задается по два целых числа – пары кружков, соединенных отрезками.
Выведите одну строку, состоящую из n символов из множества {'R', 'G', 'B'} – цвета кружков после перекраски. Если решений несколько, выведите любое.
Если решения не существует, выведите слово "Impossible''.
4 5 RRRG 1 3 1 4 3 4 2 4 2 3
GGBR
4 5 RGRR 1 3 1 4 3 4 2 4 2 3
Impossible
При расследовании дорожно-транспортных происшествий часто возникают проблемы с розыском автомобилей, водители которых покинули место происшествия.
Получение свидетельских показаний – непростая работа. Ситуация осложняется тем, что очень часто свидетели могут только приблизительно вспомнить номер автомобиля. При этом с большой вероятностью опрашиваемый может перепутать порядок цифр или букв в номере.
По полученному от свидетеля происшествия номеру, подсчитайте, сколько различных номеров может получиться из него перестановкой букв и/или цифр, а также выведите все такие номера.
Напомним, что автомобильные номера в России состоят из трех букв и трех цифр, упорядоченных следующим образом: буква, три цифры, затем две буквы. Фрагмент номера, который идентифицирует регион, в котором зарегистрирован автомобиль, мы будем игнорировать.
В номере могут использоваться следующие буквы: «A», «B», «C», «E», «H», «K», «M», «O», «P», «T», «X», «Y» (эти буквы имеют схожие по написанию аналоги как в русском, так и в латинском алфавите). В этой задаче во входных данных будут использоваться буквы латинского алфавита.
На вход программы поступает одна строка, которая представляет собой корректный автомобильный номер.
В первой строке выведите число k – количество номеров, которые могут получиться из заданного перестановкой букв и/или цифр.
В последующих k строках выведите все такие номера в произвольном порядке.
X772KX
9 X277XK X277KX X727XK X727KX X772XK X772KX K277XX K727XX K772XX
Известно, что сложение и умножение являются ассоциативными операциями. Это значит, что значение выражений вида \(a_1\) + \(a_2\) +...+ \(a_n\) и \(a_1\) . \(a_2\) . ... . \(a_n\) не зависит от порядка выполнения в них действий и, следовательно, не меняется при произвольной расстановке в этих выражениях скобок.
В отличие от сложения и умножения, деление – операция не ассоциативная. Так, значение выражения вида \(a_1\)/\(a_2\)/ ... /\(a_n\) может меняться при расстановке в нем скобок.
Рассмотрим выражение вида
\(p_1\)/\(p_2\)/ ... /\(p_n\),
где все \(p_i\) – простые числа (не обязательно различные). Найдите количество возможных значений, которые может принять указанное выражение после расстановки в нем скобок, а также количество целых чисел среди этих значений.
Например, выражение 3/2/2 после расстановки скобок может принять два значения: 3/4 = (3/2)/2 и 3 = 3/(2/2).
В первой строке вводится число \(n\) ( 1\( \le\)n\( \le\)200). Следующая строка содержат \(n\) натуральных чисел – \(p_1\), \(p_2\),..., \(p_n\). Все числа \(p_i\) простые и не превосходят \(10^4\).
В первой строке выведите количество возможных значений, которые может принять выражение \(p_1\)/\(p_2\)/ ... /\(p_n\) при заданных \(p_i\) после расстановки в нем скобок. Во второй строке выведите количество целых чисел среди этих значений.
3 3 2 2
2 1