При расследовании дорожно-транспортных происшествий часто возникают проблемы с розыском автомобилей, водители которых покинули место происшествия.

Получение свидетельских показаний – непростая работа. Ситуация осложняется тем, что очень часто свидетели могут только приблизительно вспомнить номер автомобиля. При этом с большой вероятностью опрашиваемый может перепутать порядок цифр или букв в номере.

По полученному от свидетеля происшествия номеру, подсчитайте, сколько различных номеров может получиться из него перестановкой букв и/или цифр, а также выведите все такие номера.

Напомним, что автомобильные номера в России состоят из трех букв и трех цифр, упорядоченных следующим образом: буква, три цифры, затем две буквы. Фрагмент номера, который идентифицирует регион, в котором зарегистрирован автомобиль, мы будем игнорировать.

В номере могут использоваться следующие буквы: «A», «B», «C», «E», «H», «K», «M», «O», «P», «T», «X», «Y» (эти буквы имеют схожие по написанию аналоги как в русском, так и в латинском алфавите). В этой задаче во входных данных будут использоваться буквы латинского алфавита.

Известно, что сложение и умножение являются ассоциативными операциями. Это значит, что значение выражений вида \(a_1\) + \(a_2\) +...+ \(a_n\) и \(a_1\) . \(a_2\) . ... . \(a_n\) не зависит от порядка выполнения в них действий и, следовательно, не меняется при произвольной расстановке в этих выражениях скобок.

В отличие от сложения и умножения, деление – операция не ассоциативная. Так, значение выражения вида \(a_1\)/\(a_2\)/ ... /\(a_n\) может меняться при расстановке в нем скобок.

Рассмотрим выражение вида

\(p_1\)/\(p_2\)/ ... /\(p_n\),

где все \(p_i\) – простые числа (не обязательно различные). Найдите количество возможных значений, которые может принять указанное выражение после расстановки в нем скобок, а также количество целых чисел среди этих значений. Например, выражение 3/2/2 после расстановки скобок может принять два значения: 3/4 = (3/2)/2 и 3 = 3/(2/2).

В компании QQQ работает n человек. Очередной проект компании состоит из m независимых частей. Управляющий компании оценил время, которое требуется для выполнения каждой из частей проекта (предполагается, что это время не зависит от того, кто будет выполнять эту часть). После чего он некоторым образом распределил все m частей между n работниками. В результате оказалось, что некоторым из работников потребуется потратить на выполнение своей работы больше времени, чем другим (поскольку им досталась более объемная работа).

Поэтому управляющий решил улучшить распределение работ следующим образом: выбрать двух различных работников и выбрать одну из частей проекта, назначенную первому работнику, и одну из частей, назначенную второму. После этого часть проекта, назначенную первому работнику, назначить второму, а часть, назначенную второму, назначить первому. Если в результате этой операции максимум из времен выполнения работы первым и вторым работниками уменьшился, то такую операцию назовем оптимизирующей.

Например, пусть проект состоит из пяти частей со временами выполнения 3,6,4,8,2, и в компании есть три работника. Пусть распределение работ выглядит следующим образом: первый работник части 1 и 2 (суммарное время 3 + 6 = 9), второй работник часть 4 (суммарное время 8) и третий работник части 3 и 5 (суммарное время 4 + 2 = 6). Тогда если первое задание (назначенное первому работнику) назначить третьему, а пятое задание (назначенное третьему) назначить первому, то у первого работника суммарное время станет равно 6 + 2 = 8, а у третьего 3 + 4 = 7. Поскольку max(9,6) > max(8,7), то эта операция будет оптимизирующей.

Вам дано число работников в компании, число частей в проекте, время, необходимое на выполнение каждой из частей проекта и распределение частей по работникам. Требуется посчитать число различных возможных оптимизирующих операций в данном распределении работ.

Маленький Вася очень любит поезда. На день рождения ему подарили игрушечную железную дорогу. В комплект к железной дороге входит поезд, состоящий из \(n\) вагонов, пронумерованных числами от 1 до \(n\).

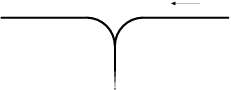
Справа к тупику подъезжает поезд, составленный из всех \(n\) вагонов. Затем вагоны по одному загоняются в сортировочный тупик и выгоняются из него налево. Васе нравится, если ему удается отсортировать поезд с помощью сортировочного тупика — добиться того, чтобы слева от тупика вагоны были расположены по порядку от 1 до \(n\).

Например, пусть в исходном поезде 4 вагона, которые следуют в порядке 3, 1, 2, 4. Его можно отсортировать следующим образом. Загоняем вагон 3 в тупик. Загоняем вагон 1 в тупик. Выгоняем вагон 1 из тупика. Загоняем вагон 2 в тупик. Выгоняем вагон 2 из тупика. Выгоняем вагон 3 из тупика. Загоняем вагон 4 в тупик. Выгоняем вагон 4 из тупика.

Не все поезда можно отсортировать таким образом. Например, поезд из 3 вагонов, следующих в порядке 2, 3, 1, отсортировать нельзя.

Вася выписал на листке в лексикографическом порядке все поезда длины \(n\), которые можно отсортировать с помощью тупика. Поезд \((a_1, a_2, \ldots, a_n)\) идет раньше поезда \((b_1, b_2, \ldots, b_n)\) в лексикографическом порядке, если существует такое \(i\) (\(1 \le i \le n\)), что для всех \(j < i\) выполняется \(a_j = b_j\), а \(a_i < b_i\). Например, все поезда из трех вагонов, которые можно отсортировать с помощью тупика, в лексикографическом порядке выписываются следующим образом: \((1, 2, 3)\), \((1, 3, 2)\), \((2, 1, 3)\), \((3, 1, 2\)), \((3, 2, 1)\).

Вася потерял свой листок, и его интересует вопрос: какой поезд был выписан на его листке под номером \(k\). Помогите ему выяснить это.

4 1

1 2 3 4

4 3

1 3 2 4

4 15

-1