Решите в целых числах уравнение:
\(\sqrt{ax+b} = c\),
a, b, c – данные целые числа: найдите все решения или сообщите, что решений в целых числах нет.
Вводятся три числа a, b и c, разделенные пробелами.
Программа должна вывести все решения уравнения в порядке возрастания, либо NO SOLUTION (заглавными буквами), если решений нет. Если решений бесконечно много, вывести MANY SOLUTIONS.
1 0 0
0
1 2 -3
NO SOLUTION
Натуральные числа записаны в (бесконечную) таблицу, как показано на рисунке.
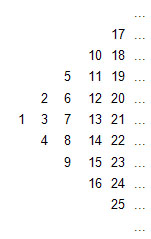
Требуется по заданному числу вывести всех его соседей (числа, записанные в клетках сверху, справа, слева и снизу, если таковые имеются)
Вводится одно натуральное число, не превосходящее \(10^9\).
Программа должна вывести все числа, записанные в соседних клетках с данным, в порядке возрастания. Числа должны разделяться пробелом.
1
3
7
3 6 8 13
Возьмем произвольное слово и проделаем с ним следующую операцию: поменяем местами его первую согласную букву с последней согласной буквой, вторую согласную букву с предпоследней согласной буквой и т.д. Если после этой операции мы вновь получим исходное слово, то будем называть такое слово негласным палиндромом. Например, слова sos, rare, rotor, gong, karaoke являются негласными палиндромами.
Вам требуется написать программу, которая по данному слову определяет, является ли оно негласным палиндромом.
Вводится строка, содержащая только строчные буквы латинского алфавита.
Программа должна вывести YES, если введенное слово является негласным палиндромом, и NO в противном случае.
tennete
YES
Вводится натуральное число. Требуется разделить запятыми тройки его цифр (считая справа).
Вводится одно натуральное число, не превышающее 10100.
Вывести то же число, разделяя тройки цифр запятыми.
1000
1,000
12345678
12,345,678
999
999
Двое играют в такую игру. Первый называет число, затем второй называет число. Если число второго больше, то он выиграл, в противном случае (даже если числа равны), выиграл первый. Помогите второму игроку – напишите программу, которая будет за него успешно играть в эту игру.
Вводится натуральное число \(A\), которое назвал первый игрок (в числе \(А\) не больше \(100\) цифр).
Выведите одно натуральное число – какой-нибудь (любой!) выигрышный ход второго игрока.
1
1000000000000000