Широкое распространение в стандартных библиотеках многих языков программирования получила реализация сбалансированных деревьев на основе так называемых красно-черных деревьев. В данной задаче вам предлагается посчитать количество красно-черных деревьев заданной формы.
Напомним, что двоичным деревом называется набор вершин, организованных в виде дерева. Каждая вершина имеет не более двух детей, один из которых называется левым, а другой – правым. Как левый, так и правый ребенок, а также оба могут отсутствовать.
Если вершина Y – ребенок вершины X, то говорят, что вершина X является родителем вершины Y. У каждой вершины дерева, кроме одной, есть ровно один родитель. Единственная вершина, не имеющая родителя, называется корнем дерева.
Соединим каждую вершину, кроме корня, с ее родителем. Заметим, что для каждой вершины существует ровно один путь, ведущий в нее от корня.
Двоичное дерево называется красно-черным, если каждая его вершина раскрашена в красный либо в черный цвет, причем выполняются следующие условия:
- если вершина красная, то ее родитель – черный;
- количество черных вершин на пути от корня до любой вершины, у которой отсутствует хотя бы один ребенок, одно и то же.
Примеры двоичного дерева, вершины которого раскрашены в два цвета, приведены на следующем рисунке.
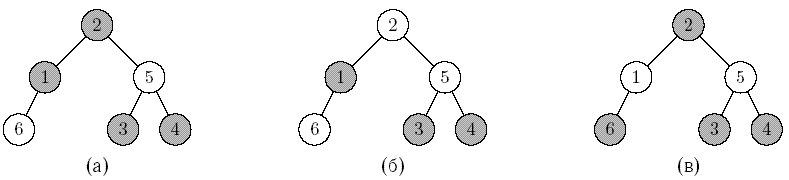 |
Если считать закрашенные вершины черными, а незакрашенные – красными, то дерево на рисунке (а) является красно-черным деревом, а деревья на рисунках (б) и (в) – нет. Для дерева на рисунке (б) нарушается первое свойство – у красной вершины 5 родитель 2 также красный, а в дереве на рисунке (в) нарушается второе свойство – на пути от корня до вершины 1 одна черная вершина, а, например, на пути от корня до вершины 3 – две.
Для заданного двоичного дерева подсчитайте число способов раскрасить его вершины в черный и красный цвет так, чтобы оно стало красно-черным деревом.
В первой строке вводится число n – количество вершин в дереве ( 1![]() n
n![]() 1000).
1000).
Пусть вершины дерева пронумерованы числами от 1 до n. Следующие n строк содержат по два числа – для каждой вершины заданы номера ее левого и правого ребенка. Если один из детей отсутствует, то вместо его номера записан ноль. Гарантируется, что входные данные корректны, то есть набор вводимых чисел действительно задает двоичное дерево.
Выведите одно число – количество способов раскрасить вершины заданного двоичного дерева в красный и черный цвета так, чтобы оно стало красно-черным деревом.
 |
6 6 0 1 5 0 0 0 0 3 4 0 0
3
4 2 0 3 0 4 0 0 0
0
Вася любит искать во всём закономерности. В его тетрадке записаны три числа A,B и C, и он хочет установить между ними какую-нибудь простую закономерность. Для начала он хочет узнать, можно ли этим числам приписать в конец несколько нулей так, чтобы сумма первых двух чисел стала равна третьему. Например, если у него записаны числа 9,34 и 43, то он может не приписывать к ним нулей сумма 9 и 34 и так равна 43. Если же у него записаны числа 23, 7 и 93, то он может приписать нуль к 7 и получить 70. После чего 23 + 70 = 93. Вам дано три натуральных числа A,B и C. Требуется найти неотрицательные целые числа n, m и k, такие что A × 10n + B × 10m = C × 10k.
На первой строке входного файла записано число A, на второй B, на третьей C. Все числа не меньше единицы и не больше 10100000.
Если числа n, m и k, удовлетворяющие условию, существует — выведите на первой строке YES, а на второй строке сами числа. Числа должны быть неотрицательными и не превосходить 106. Если решений несколько — выведите любое. Если же таких чисел не существует — выведите NO.
9 34 43
YES 0 0 0
23 7 93
YES 0 1 0
1 2 4
NO
У Пети имеется неограниченный набор красных, синих и зеленых плиток размером 1×1. Он выбирает ровно N плиток и выкладывает их в полоску. Например, при N = 10 она может выглядеть следующим образом:
| К | К | К | С | З | К | К | З | К | С |
(Буквой К обозначена красная плитка, С – синяя, З – зеленая)
После этого Петя заполняет следующую таблицу:
|
| красный | синий | зеленый |
| красный | Y | Y | Y |
| синий | Y | N | Y |
| зеленый | Y | Y | N |
В клетке на пересечении строки, отвечающей цвету А, и столбца, отвечающего цвету Б, он записывает "Y", если в его полоске найдется место, где рядом лежат плитки цветов А и Б и "N" в противном случае. Считается, что плитки лежат рядом, если у них есть общая сторона. (Очевидно, что таблица симметрична относительно главной диагонали – если плитки цветов А и Б лежали рядом, то рядом лежали и плитки цветов Б и А.) Назовем такую таблицу диаграммой смежности данной полоски.
Так, данная таблица представляет собой диаграмму смежности приведенной выше полоски.
Петя хочет узнать, сколько различных полосок имеет определенную диаграмму смежности. Помогите ему.
(Заметьте, что полоски, являющиеся отражением друг друга, но не совпадающие, считаются разными. Так, полоска
| С | К | З | К | К | З | С | К | К | К |
не совпадает с полоской, приведенной в начале условия.)
Формат входных данных
Первая строка входного файла содержит число N. (1 N 100). Следующие три строки входного файла, содержащие по три символа из набора {"Y", "N"}, соответствуют трем строкам диаграммы смежности. Других символов, включая пробелы, во входном файле не содержится. Входные данные корректны, т.е. диаграмма смежности симметрична.
Формат выходных данных
Выведите в выходной файл количество полосок длины N, имеющих приведенную во входном файле диаграмму смежности.
Примеры
| Входные данные | Выходные данные |
| 10 YYY YNY YYN | 4596 |
| 3 YYY YYY YYY | 0 |