На клеточном поле, размером \(N\)x\(M\) (2 ≤ \(N\), \(M\) ≤ 250) сидит \(Q\) (0 ≤ \(Q\) ≤ 10000) блох в различных клетках. "Прием пищи" блохами возможен только в кормушке - одна из клеток поля, заранее известная. Блохи перемещаются по полю странным образом, а именно, прыжками, совпадающими с ходом обыкновенного шахматного коня. Длина пути каждой блохи до кормушки определяется как количество прыжков. Определить минимальное значение суммы длин путей блох до кормушки или, если собраться блохам у кормушки невозможно, то сообщить об этом. Сбор невозможен, если хотя бы одна из блох не может попасть к кормушке.

Отделу космических исследований поступило задание сфотографировать из космоса \(n\) объектов в заданной области. Область имеет форму квадрата размером \(50\times 50\) километров. Если разделить ее на квадраты размером \(1\times 1\) километр, то интересующие отдел объекты окажутся в центрах некоторых единичных квадратов.

Введем систему координат, направив ось OX с запада на восток и ось OY с юга на север. Тогда каждому единичному квадрату будут сопоставлены координаты в диапазоне от 1 до 50, как показано на рисунке ниже.

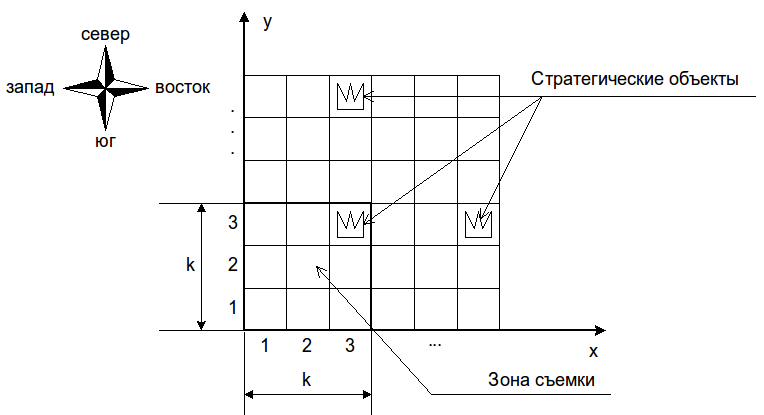
Для космической съемки используется специальный фотоаппарат высокого разрешения, установленный на космическом спутнике. Фотоаппарат может делать снимки квадратных участков земной поверхности размером \(k\times k\) километров. Исходно аппарат наведен на юго-западный угол заданной области, то есть, если сделать снимок, на нем будут видны единичные квадраты с координатами \(x\) и \(y\) от \(1\) до \(k\) километров.

С помощью специальных двигателей можно изменять орбиту спутника, что приводит к изменению участка съемки. За один день орбиту спутника можно изменить таким образом, что участок съемки сместится либо на один километр на запад, либо на один километр на восток, либо на один километр на север. Переместить участок съемки на юг невозможно. Непосредственно между перемещениями спутника можно сделать снимок, временем съемки можно пренебречь.

Руководство отдела заинтересовалось вопросом: за какое минимальное количество дней можно сделать снимки всех объектов заданной области.

Требуется написать программу, которая по заданному расположению объектов и размеру снимка \(k\) определит минимальное время, за которое можно сделать снимки всех объектов заданной области.