Темы --> Информатика --> Алгоритмы --> Алгоритмы на графах --> Кратчайшие пути в графе --> Обход в ширину
    0-1 BFS(3 задач)
---> 7 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: 1 2 >> Отображать по:
#14
Сталкер
  
Темы: [0-1 BFS]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
128 megabytes

В городе Н при невыясненных обстоятельствах территория одного из заводов превратилась в аномальную зону. Все подъезды к территории были перекрыты, а сама она получила название промзоны. В промзоне находятся N зданий, некоторые из них соединены дорогами. По любой дороге можно перемещаться в обоих направлениях.

Начинающий сталкер получил задание добраться до склада в промзоне. Он нашел в электронном архиве несколько карт территории промзоны. Так как карты составлялись разными людьми, то на каждой из них есть информация только о некоторых дорогах промзоны. Одна и та же дорога может присутствовать на нескольких картах.

В пути сталкер может загружать из архива на мобильный телефон по одной карте. При загрузке новой карты предыдущая в памяти телефона не сохраняется. Сталкер может перемещаться лишь по дорогам, отмеченным на карте, загруженной на данный момент. Каждая загрузка карты стоит 1 рубль. Для минимизации расходов сталкеру нужно выбрать такой маршрут, чтобы как можно меньшее число раз загружать карты. Сталкер может загружать одну и ту же карту несколько раз, при этом придется заплатить за каждую загрузку. Изначально в памяти мобильного телефона нет никакой карты.

Требуется написать программу, которая вычисляет минимальную сумму расходов, необходимую сталкеру, чтобы добраться от входа в промзону до склада.

Входные данные

В первой строке входных данных содержатся два натуральных числа N и K (2 ≤ N ≤ 2000; 1 ≤ K ≤ 2000) — количество зданий промзоны и количество карт соответственно. Вход в промзону находится в здании с номером 1, а склад — в здании с номером N.

В последующих строках находится информация об имеющихся картах. Первая строка описания i-ой карты содержит число ri — количество дорог, обозначенных на i-ой карте. Затем идут ri строк, содержащие по два натуральных числа a и b (1 ≤ a, b ≤ N; a ≠ b), означающих наличие на i-ой карте дороги, соединяющей здания a и b. Суммарное количество дорог, обозначенных на всех картах, не превышает 300 000 (r1 + r2 + … + rK ≤ 300 000).

Выходные данные

Выведите одно число — минимальную сумму расходов сталкера. В случае, если до склада добраться невозможно, выведите число –1.

Примеры
Входные данные
12 4
4
1 6
2 4
7 9
10 12
3
1 4
7 11
3 6
3
2 5
4 11
8 9
5
3 10
10 7
7 2
12 3
5 12
Выходные данные
3
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

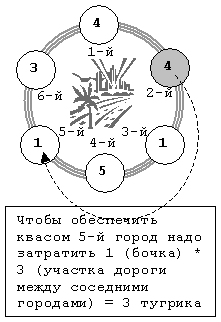
Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
#1203
Кенгуренок Лео
  
#1653
Бусинки
  
ограничение по времени на тест
0.3 second;
ограничение по памяти на тест
64 megabytes

Маленький мальчик делает бусы. У него есть много пронумерованных бусинок. Каждая бусинка имеет уникальный номер – целое число в диапазоне от 1 до N. Он выкладывает все бусинки на полу и соединяет бусинки между собой произвольным образом так, что замкнутых фигур не образуется. Каждая из бусинок при этом оказывается соединенной с какой-либо другой бусинкой.
Требуется определить, какое максимальное количество последовательно соединенных бусинок присутствует в полученной фигуре (на рисунке эти бусинки выделены темным цветом).

Формат входных данных

В первой строке – количество бусинок 1≤N≤2500. В последующих N-1 строках по два целых числа – номера, соединенных бусинок.

Формат выходных данных

Вывести одно число – искомое количество бусинок.

Пример

Входные данные

Выходные данные

7

4 5

6 7

7 4

7 2

1 3

4 1

5
#1668
Блохи
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Блохи сидят на клетках шахматного поля и ходят конем. Должны собраться в одной из клеток. Определить сумму длин кратчайших путей.

На клеточном поле, размером \(N\)x\(M\) (2 ≤ \(N\), \(M\) ≤ 250) сидит \(Q\) (0 ≤ \(Q\) ≤ 10000) блох в различных клетках. "Прием пищи" блохами возможен только в кормушке - одна из клеток поля, заранее известная. Блохи перемещаются по полю странным образом, а именно, прыжками, совпадающими с ходом обыкновенного шахматного коня. Длина пути каждой блохи до кормушки определяется как количество прыжков. Определить минимальное значение суммы длин путей блох до кормушки или, если собраться блохам у кормушки невозможно, то сообщить об этом. Сбор невозможен, если хотя бы одна из блох не может попасть к кормушке.

Входные данные

В первой строке входного файла находится 5 чисел, разделенных пробелом: \(N\), \(M\), \(S\), \(T\), \(Q\). \(N\), \(M\) - размеры доски (отсчет начинается с 1); \(S\), \(T\) - координаты клетки - кормушки (номер строки и столбца соответственно), \(Q\) - количество блох на доске. И далее \(Q\) строк по два числа - координаты каждой блохи.

Выходные данные

Содержит одно число - минимальное значение суммы длин путей или -1, если сбор невозможен.

Примеры
Входные данные
2 2 1 1 1
2 2
Выходные данные
-1
Страница: 1 2 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест