Динамическое программирование на таблицах(46 задач)
Динамическое программирование по подстрокам(21 задач)
Задача о рюкзаке(34 задач)
Окружная олимпиада(18 задач)
Региональный этап(109 задач)
Заключительный этап(97 задач)
Вновь открытое казино предложило оригинальную игру.
В начале игры крупье выставляет в ряд несколько фишек разных цветов. Кроме того, он объявляет, какие последовательности фишек игрок может забирать себе в процессе игры. Далее игрок забирает себе одну из заранее объявленных последовательностей фишек, расположенных подряд. После этого крупье сдвигает оставшиеся фишки, убирая разрыв. Затем игрок снова забирает себе одну из объявленных последовательностей и так далее. Игра продолжается до тех пор, пока игрок может забирать фишки.
Рассмотрим пример. Пусть на столе выставлен ряд фишек rrrgggbbb, и крупье объявил последовательности rg и gb. Игрок, например, может забрать фишки rg, лежащие на третьем и четвёртом местах слева. После этого крупье сдвинет фишки, и на столе получится ряд rrggbbb. Ещё дважды забрав фишки rg, игрок добьётся того, что на столе останутся фишки bbbи игра закончится, так как игроку больше нечего забрать со стола. Игрок мог бы действовать и по-другому — на втором и третьем ходах забрать не последовательности rg, а последовательности gb. Тогда на столе остались бы фишки rrb. Аналогично, игрок мог бы добиться того, чтобы в конце остались ряды rrr или rbb.
После окончания игры полученные фишки игрок меняет на деньги. Цена фишки зависит от её цвета.
Требуется написать программу, определяющую максимальную сумму, которую сможет получить игрок.
В первой строке входных данных содержится число K (1 ≤ K ≤ 26) — количество цветов фишек. Каждая из следующих K строк начинается со строчной латинской буквы, обозначающей цвет. Далее в той же строке через пробел следует целое число Xi (1 ≤ Xi ≤ 150, i = 1..K) — цена фишки соответствующего цвета.
В (K+2)-ой строке описан ряд фишек, лежащих на столе в начале игры. Ряд задаетсяL строчными латинскими буквами (1 ≤ L ≤ 150), которые обозначают цвета фишек ряда.
В следующей строке содержится число N(1 ≤ N ≤ 150) — количество последовательностей, которые были объявлены крупье. В следующих N строках записаны эти последовательности. Гарантируется, что сумма длин этих N строк не превосходит 150 символов, и все они непустые.
Выведите единственное целое число — максимальную сумму денег, которую может получить игрок.
3 v 3 l 1 u 2 luvu 3 luv vul uuu
6
Теплым весенним днем группа из N школьников-программистов гуляла в окрестностях города Кисловодска. К несчастью, они набрели на большую и довольно глубокую яму. Как это случилось — непонятно, но вся компания оказалась в этой яме.
Глубина ямы равна H. Каждый школьник знает свой рост по плечи hi и длину своих рук li. Таким образом, если он, стоя на дне ямы, поднимет руки, то его ладони окажутся на высоте hi + li от уровня дна ямы. Школьники могут, вставая друг другу на плечи, образовывать вертикальную колонну. При этом любой школьник может встать на плечи любого другого школьника. Если под школьником i стоят школьники j1, j2, …, jk, то он может дотянуться до уровня hj1 + hj2 + … + hjk + hi + li.
Если школьник может дотянуться до края ямы (то есть hj1 + hj2 + … + hjk + hi + li ≥ H), то он может выбраться из нее. Выбравшиеся из ямы школьники не могут помочь оставшимся.
Найдите наибольшее количество школьников, которые смогут выбраться из ямы до прибытия помощи, и перечислите их номера.
В первой строке входных данных задается натуральное число N (1 ≤ N ≤ 2000) — количество школьников, попавших в яму.
Далее в N строках содержится по два целых числа: рост i-го школьника по плечи hi (1 ≤ hi ≤ 105) и длина его рук li (1 ≤ li ≤ 105).
В последней строке указано целое число — глубина ямы H (1 ≤ H ≤ 105).
В первой строке выведите K — максимальное количество школьников, которые смогут выбраться из ямы. Если K > 0, то во второй строке в произвольном порядке выведите их номера, разделяя их пробелами. Школьники нумеруются с единицы в том порядке, в котором они заданы во входных данных. Если существует несколько решений, выведите любое.
Примечание
Решение, дающее правильный ответ только при N ≤ 100; H, hi, li ≤ 1000, будет оцениваться из 70 баллов.
1 239 239 566
0
3 1 2 1 2 4 1 7
2 2 1
Юный информатик стал исследовать, как изменяются суммы цифр натуральных чисел при умножении и делении на разные однозначные числа. Однажды он задался вопросом, можно ли восстановить число A, если нам известна сумма его цифр, а также сумма цифр числа D×A, где D — заданное однозначное число. Довольно быстро он установил, что для восстановления числа А этой информации недостаточно. Так, например, у чисел 9 и 45 одинаковые суммы цифр. Если же их умножить на 5, то получим числа 45 и 225, которые тоже имеют одинаковые суммы цифр.
Тогда юный информатик стал искать ответ на поставленный вопрос при условии, что нам известно K — количество десятичных знаков в числе A. К сожалению, и тут его ждало разочарование. У некоторых чисел, имеющих одинаковое количество цифр и одинаковые суммы цифр, после умножения на один и тот же множитель эти суммы опять оказываются одинаковыми. Такими числами, например, являются 42 и 51 при D = 3.
И тогда юный информатик поставил перед собой такую задачу: найти наименьшее K значное натуральное число A в десятичной системе счисления, которое имеет сумму цифр, равную S, а число D×A имеет сумму цифр, равную P.
Требуется написать программу, решающую поставленную задачу.
Вводятся четыре натуральных числа K, S, P, D (1 ≤ K ≤ 100, 1 ≤ S ≤ 9K, 1 ≤ P ≤ 9(K+1), 1 ≤ D ≤ 9).
Выведите число A, если оно существует, или –1, в противном случае. Число A не может начинаться с нуля.
Примечание
Решения, корректно работающие при K ≤ 40, будут оцениваться, исходя из 80 баллов.
3 15 15 1
159
Рассмотрим прямоугольную таблицу размером n m. Занумеруем строки таблицы числами от 1 до n, а столбцы – числами от 1 до m. Будем такую таблицу последовательно заполнять числами следующим образом.
Обозначим через aij число, стоящее на пересечении i-ой строки и j-ого столбца. Первая строка таблицы заполняется заданными числами – a11, a12, …, a1m. Затем заполняются строки с номерами от 2 до n. Число aij вычисляется как сумма всех чисел таблицы, находящихся в «треугольнике» над элементом aij. Все вычисления при этом выполняются по модулю r.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ai,j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Более точно, значение aij вычисляется по следующей формуле:
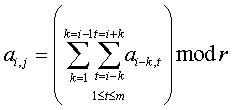
Например, если таблица состоит из трех строк и четырех столбцов, и первая строка состоит из чисел 2,3,4,5, а r = 40 то для этих исходных данных таблица будет выглядеть следующим образом (взятие по модулю показано только там, где оно приводит к изменению числа):
| 2 | 3 | 4 | 5 |
| 5 = 2 + 3 | 9 = 2 + 3 + 4 | 12 = 3 + 4 + 5 | 9 = 4 + 5 |
| 23 = 2 + 3 + 4 + 5 + 9 | 0 = (2 + 3 + 4 + 5 + 5 + 9 + 12) mod 40 = 40 mod 40 | 4 = (2 + 3 + 4 + 5 + 9 + 12 + 9) mod 40 = 44 mod 40 | 33 = 3 + 4 + 5 + 12 + 9 |
Требуется написать программу, которая по заданной первой строке таблицы (a11, a12, …, a1m), вычисляет последнюю строку, как описано выше.
Первая строка входного файла содержит числа n, m и r (2 ≤ n, m ≤ 2000, 2 ≤ r ≤ 109) – число строк и столбцов таблицы соответственно, а так же число, по модулю которого надо посчитать ответ. Следующая строка содержит m целых чисел – первую строку таблицы: a11, a12, …, a1m. Все a1i неотрицательны и не превосходят 109.
В первой строке выходного файла необходимо вывести m чисел – последнюю строку таблицы: an1, an2, …, anm.
2 3 10 1 2 3
3 6 5
3 3 10 1 1 1
8 0 8
3 4 40 2 3 4 5
23 0 4 33