С детства Максим был неплохим музыкантом и мастером на все руки. Недавно он самостоятельно сделал несложный перкуссионный музыкальный инструмент — треугольник. Ему нужно узнать, какова частота звука, издаваемого его инструментом.

У Максима есть профессиональный музыкальный тюнер, с помощью которого можно проигрывать ноту с заданной частотой. Максим действует следующим образом: он включает на тюнере ноты с разными частотами и для каждой ноты на слух определяет, ближе или дальше она к издаваемому треугольником звуку, чем предыдущая нота. Поскольку слух у Максима абсолютный, он определяет это всегда абсолютно верно.

Вам Максим показал запись, в которой приведена последовательность частот, выставляемых им на тюнере, и про каждую ноту, начиная со второй, записано — ближе или дальше она к звуку треугольника, чем предыдущая нота. Заранее известно, что частота звучания треугольника Максима составляет не менее 30 герц и не более 4000 герц.

Требуется написать программу, которая определяет, в каком интервале может находиться частота звучания треугольника.

Предприятие «Авто-2010» выпускает двигатели для известных во всём мире автомобилей. Двигатель состоит ровно из \(n\) деталей, пронумерованных от 1 до \(n\), при этом деталь с номером \(i\) изготавливается за \(p_i\) секунд. Специфика предприятия «Авто-2010» заключается в том, что там одновременно может изготавливаться лишь одна деталь двигателя. Для производства некоторых деталей необходимо иметь предварительно изготовленный набор других деталей.

Генеральный директор «Авто-2010» поставил перед предприятием амбициозную задачу — за наименьшее время изготовить деталь с номером 1, чтобы представить её на выставке.

Требуется написать программу, которая по заданным зависимостям порядка производства между деталями найдёт наименьшее время, за которое можно произвести деталь с номером 1.

В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.

Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.

К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.

Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.

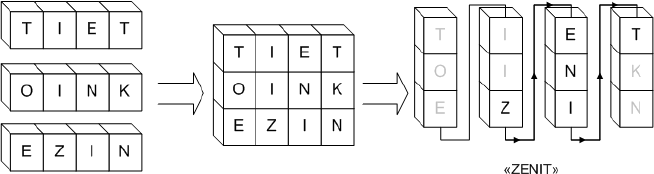
После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».

Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.

Начинающий программист Поликарп очень любит дарить подарки, особенно в коробках. Он давно заметил, что если коробка красиво оформлена, то радость от подарка возрастает многократно. Любой обёрточной бумаге он предпочитает клетчатую. В самом деле, после распаковки подарка на ней можно играть в крестики-нолики, морской бой, точки, а также решать задачи и писать программы.

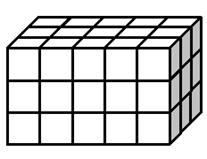
Поликарп очень аккуратен. Он упаковывает подарок в коробку, имеющую форму прямоугольного параллелепипеда, и оклеивает всю её поверхность клетчатой бумагой. При этом каждая грань коробки представляет собой прямоугольник, состоящий из целых клеток. На рисунке изображён пример такой упаковки подарка.

В настоящий момент Поликарп собирается поздравить свою подругу, недавно вернувшуюся с очередной олимпиады. Он хочет подарить ей подарок в большой и красивой коробке.

У Поликарпа в наличии есть лист клетчатой бумаги, состоящий из \(n\) клеток. Каким будет максимальный объём коробки, которую можно оклеить с использованием этого листа бумаги описанным выше способом? Поликарп может разрезать лист клетчатой бумаги по границам клеток произвольным образом и оклеивать коробку получившимися фигурами, поэтому форма листа не важна, а имеет значение только количество клеток на нём. Поликарп может использовать для оклеивания коробки не все клетки.

Напишите программу, которая по заданному количеству клеток \(n\) находит размеры коробки максимального возможного объема.

Ханты-Мансийский автономный округ — Югра является важнейшим нефтяным регионом России. Добыча нефти составляет 267 млн т в год, её транспортировка осуществляется по трубопроводам, общая длина которых превышает длину экватора Земли.

Система транспортировки нефти представляет собой совокупность \(n\) распределительных станций и \(m\) трубопроводов. Каждый трубопровод соединяет две различные станции. Между любыми двумя станциями проложено не более одного трубопровода.

Эффективность работы станций существенно зависит от вязкости нефти. Поэтому компания «ЮграНефтеТранс», в ведении которой находится сеть трубопроводов, заказала инновационному исследовательскому предприятию разработку и изготовление новых сверхточных датчиков вязкости на основе самых современных технологий.

Изготовление датчиков — процесс трудоёмкий и дорогостоящий, поэтому было решено изготовить \(k\) датчиков (\(k\le40\)) и выбрать \(k\) различных станций, на которых датчики будут установлены. Необходимо осуществить выбор станций так, чтобы датчики контролировали все трубопроводы: для каждого трубопровода хотя бы один датчик должен быть установлен на станции, где начинается или заканчивается этот трубопровод.

Напишите программу, которая проверяет, существует ли требуемое расположение датчиков, и в случае положительного ответа находит это расположение.