Темы
    Информатика(2656 задач)
---> 304 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 39 40 41 42 43 44 45 >> Отображать по:
#111494
Две окружности
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью небольших камушков. Митя разложил на поле n камушков так, чтобы каждый из них находился на одной из окружностей или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности размещался хотя бы один камушек. Обладая великолепным глазомером, Митя расположил камушки на окружностях абсолютно точно, без какой-либо погрешности.

На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем которого он был, то есть, восстановить окружности.

Требуется написать программу, которая по координатам камушков на поле находит вариант размещения их на двух несовпадающих окружностях.

Входные данные

Первая строка входного файла содержит целое число n — количество размещенных Митей камушков на поле (\(2 \leq n \leq 2000\)). Последующие n строк содержат целочисленные координаты (\(x_i\), \(y_i\)) камушков — по одной паре координат, разделенных пробелом, в каждой строке (\(−10^6 \leq x_i, y_i \leq 10^6\)). Никакие два камушка не размещаются в одной точке.

Гарантируется, что ответ для заданного набора камушков существует.

Выходные данные

Выходной файл должен содержать две строки. Первая строка должна содержать последовательность номеров всех камушков, которые принадлежат первой окружности, вторая строка — последовательность номеров всех камушков, которые принадлежат второй окружности.

Каждый камушек должен встречаться хотя бы в одной из двух последовательностей. Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей. Считается, что камушки пронумерованы от 1 до n в порядке их следования во входных данных.

Нумерация окружностей не имеет значения, то есть выводить две последовательности можно в любом порядке. Числа в последовательностях можно также выводить в произвольном порядке. Каждая из последовательностей должна содержать не менее одного числа. Все числа в строках должны быть разделены пробелами.

Если вариантов расположения окружностей несколько, можно выбрать любой из них.

Система оценивания

Правильные решения для тестов, в которых 2 ≤ n ≤ 50, будут оцениваться из 50 баллов.

Примеры
Входные данные
7
1 -1
0 0
1 1
3 1
3 -1
2 0
4 0
Выходные данные
1 2 3 6 
4 5 6 7
Входные данные
5
-1000000 0
0 1000000
1000000 0
0 -1000000
0 0
Выходные данные
1 2 3 4 
5
#111495
Столицы
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности управления страной, выполненных ведущими экономистами Триландии.

Всего в Триландии n городов, из которых некоторые пары городов соединены дорогами, и по каждой из них можно проехать в обе стороны. Время проезда по каждой дороге в одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из каждого города можно добраться в любой другой, причем это можно сделать единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.

Как показали результаты проведенных триландскими экономистами исследований, управление страной будет наиболее эффективным, если три столицы будут выбраны так, что время кратчайшего пути между каждой парой столиц составит ровно d часов. Перед проведением выборов необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам. Две тройки городов считаются различными, если в первой тройке есть хотя бы один город, которого нет во второй тройке, и наоборот.

Требуется написать программу, которая по количеству городов в Триландии и описанию дорог находит количество троек городов, которые могут быть столицами.

Входные данные

Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии n и требуемое время в пути между столицами d (\(3 \leq n \leq 10^5\), \(1 \leq d < n\)). Каждая из последующих (n – 1) строк содержит описание одной дороги: пару разделенных пробелом различных целых чисел \(a_i\) и \(b_i\) — номера городов, которые соединены двусторонней дорогой (\(1 \leq a_i \leq n\), \(1 \leq b_i \leq n\), \(a_i \ne b_i\)). Каждая пара городов соединена не более чем одной дорогой.

Выходные данные

Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут быть выбраны столицами. В случае, если нужных троек городов не окажется, выходной файл должен содержать ноль.

Пояснения к тестам

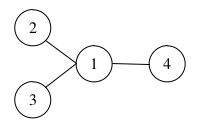
В первом примере существует единственный способ выбрать три столицы: города под номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.

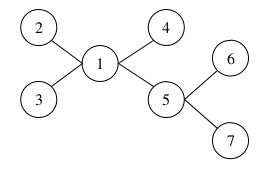
Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.

Система оценивания

Правильные решения для тестов, в которых 3 ≤ n ≤ 50, будут оцениваться из 20 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 500, будут оцениваться из 40 баллов.

Правильные решения для тестов, в которых 3 ≤ n ≤ 5000, будут оцениваться из 60 баллов.

Примеры
Входные данные
4 2
1 2
1 3
1 4
Выходные данные
1
Входные данные
7 2
1 2
1 3
1 4
5 1
5 6
5 7
Выходные данные
5
#111562
Ёжик в тумане
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

Ёжик спустился в туман и оказался в прямоугольной долине размером N на M метров, по которой бродит Лошадь. Ёжик хочет ее найти. Будем считать, что в каждый момент времени и Ёжик, и Лошадь находятся в одной из N × M клеток. Туман настолько густой, что Лошадь не видно, даже если она находится в той же самой клетке , что и Ёжик. К счастью Ёжик обладает очень острым слухом и может понять, в каком направлении сместилась Лошадь. Он также может позвать Лошадь, и, если она находится в одной клетке с Ёжиком, то Лошадь его услышит и обязательно отзовется.

В каждый момент времени Ёжик может сместиться в соседнюю клетку по горизонтали, вертикали или диагонали. Потом он отчетливо слышит, куда сместилась Лошадь относительно своего старого местоположения. Лошадь за единицу времени смещается на одну клетку только по горизонтали или вертикали (влево, вверх, вправо или вниз). При этом Лошадь не выходит за границы долины, поэтому и Ёжик не должен этого делать.

Требуется написать программу, которая поможет Ёжику, знающему свое начальное положение и следящему за передвижениями Лошади, как можно быстрее ее найти. Это интерактивная задача. В процессе тестирования программа-решение будет взаимодействовать с использованием стандартных потоков ввода/вывода с программой, моделирующей поведение лошади.

Протокол взаимодействия

Сначала программа-решение должна прочитать из стандартного потока ввода натуральные числа N и M, записанные в первой строке, а из второй строки координаты начального местоположения Ёжика – два натуральных числа: x0 – номер столбца, y0 – номер строки (1 ≤ x0 ≤ M, 1 ≤ y0 ≤ N). Числа в каждой строке разделены пробелом. Затем программа-решение начинает взаимодействие с программой, моделирующей поведение лошади, в соответствии со следующим протоколом:

1. Программа выводит в стандартный поток вывода одну строку, описывающую ход Ёжика, которая содержит три числа: его перемещение в виде указания смещения по горизонтали dx (dx = –1, 0 или 1) и по вертикали dy (dy = –1, 0 или 1), а также число 1, если Ёжик зовет Лошадь в клетке, в которую он при этом попадет, или 0 – если не зовет. Вывод должен завершаться переводом строки и сбросом буфера потока вывода. Для этого используйте

  • flush(output) в паскале или Delphi;
  • fflush(stdout) или cout.flush() в С/C++;
  • Console.out.flush() в Visual Basic.

2. После этого программа должна считать из стандартного потока ввода ответ программы, сообщающей о действии Лошади. Ответ состоит из трех чисел, расположенных в одной строке через пробел. Первое число ответа может быть равно 0 или 1, где

  • 0 означает, что Ёжик не пытался позвать Лошадь либо позвал, но Лошади в его клетке нет. В этом случае следующие два числа обозначают очередное смещение Лошади по горизонтали dx (dx = –1, 0 или 1) и по вертикали dy (dy = –1, 0 или 1), при этом хотя бы одно из значений dx или dy равно нулю;
  • 1 означает, что Ёжик позвал Лошадь, и она действительно оказалась в той же клетке, что и он. В этом случае другие два числа равны 0, и программа-решение должна закончить свою работу.

    Программа-решение не должна делать более 10 000 ходов.

Пример взаимодействия

Входные данные
2 3
1 2
0 1 0
0 0 0
1 0 0
Выходные данные

0 0 1
1 -1 0
1 0 1

Примечание

Ёжик находился в клетке (1, 2). Сначала он попробовал позвать Лошадь в той же клетке (вывод: 0 0 1), но Лошади там не оказалось, и она сместилась вправо (ввод: 0 1 0). Ёжик сместился по диагонали, но Лошадь звать не стал (вывод: 1 –1 0), а Лошадь осталась на месте (ввод: 0 0 0). Ежик сместился вправо и позвал Лошадь (вывод: 1 0 1). Лошадь оказалась в той же клетке и отозвалась (ввод: 1 0 0). Значит, изначально Лошадь находилась в клетке (2, 1), а встретились они в клетке (3, 1). Ёжик при этом сделал три хода и дважды запросил местоположение Лошади.

В данной задаче две подзадачи. Каждый тест в обеих подзадачах оценивается отдельно. Оценка за тест вычисляется по формуле min{10, round(10 × (J / S)2)}, где 10 – оценка в баллах за тест, S – количество ходов, которое потребовалось программе-решению, чтобы обнаружить Лошадь, J – количество ходов, которое требуется заданному эталонному решению при том же начальном положении Ёжика. Округление ведется по правилам математики.

  1. (оценивается в 40 баллов) 2 ≤ N, M ≤ 10.

  2. (оценивается в 60 баллов) 2 ≤ N, M ≤ 30. В этой подзадаче количество запросов о том, есть ли Лошадь в текущей клетке, не должно превышать N × M.

#111633
Хоккей на Урале
  
ограничение по времени на тест
5.0 second;
ограничение по памяти на тест
256 megabytes

Для популяризации хоккея и повышения мастерства хоккейных команд Урала был организован Всеуральский турнир. Для участия в турнире были приглашены N хоккейных команд из городов Урала.

После первых двух туров, в каждом из которых каждая команда провела по одному матчу, оказалось, что команд слишком много. Организаторами турнира было решено допустить к дальнейшему участию только K команд, никакие две из которых не встречались в рамках первых двух туров. Требуется написать программу, которая находит набор из K команд, удовлетворяющий условиям, либо выводит сообщение о том, что это сделать невозможно. В случае существования нескольких подходящих наборов необходимо найти любой из них.

Входные данные

В первой строке входного файла содержится число N (2 ≤ N ≤ 100 000, N — чётное).

Последующие N строк содержат описания всех прошедших матчей. Описание каждого матча состоит из двух натуральных чисел, не превышающих N — номеров команд, игравших в матче. Первые N / 2 из них соответствуют матчам первого тура, оставшиеся — матчам второго тура.

Последняя строка входного файла содержит одно число K (2 ≤ K ≤ N).

Гарантируется, что каждая команда сыграла ровно два матча: один в первом туре и один — во втором.

Выходные данные

Выходной файл должен содержать либо единственное число 0, если решения не существует, либо K различных чисел — номера отобранных команд.

Примечание

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.

  2. N ≤ 10. Подзадача оценивается в 30 баллов.

  3. N ≤ 1000. Подзадача оценивается в 30 баллов.

  4. N ≤ 100 000. Подзадача оценивается в 40 баллов.

Примеры
Входные данные
6
1 2
3 5
4 6
2 3
4 5
1 6
3
Выходные данные
1 3 4
Входные данные
4
1 2
3 4
2 1
4 3
3
Выходные данные
0
#111634
Робот
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
256 megabytes

Студенты одного из вузов спроектировали робота для частичной автоматизации процесса сборки авиационного двигателя.

В процессе сборки двигателя могут встречаться операции 26 типов, которые обозначаются строчными буквами латинского алфавита. Процесс сборки состоит из N операций.

Предполагается использовать робота один раз для выполнения части подряд идущих операций из процесса сборки.

Память робота состоит из K ячеек, каждая из которых содержит одну операцию. Операции выполняются последовательно, начиная с первой, в том порядке, в котором они расположены в памяти. Выполнив последнюю из них, робот продолжает работу с первой. Робота можно остановить после любой операции. Использование робота экономически целесообразно, если он выполнит хотя бы K + 1 операцию.

Требуется написать программу, которая по заданному процессу сборки определит количество экономически целесообразных способов использования робота.

Входные данные

В первой строке входного файла записано число K > 0 "— количество операций, которые можно записать в память робота.

Вторая строка состоит из N > K строчных латинских букв, обозначающих операции "— процесс сборки двигателя. Операции одного и того же типа обозначаются одной и той же буквой.

Выходные данные

Выходной файл должен содержать единственное целое число "— количество экономически целесообразных способов использования робота.

Примечание

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.

  2. N ≤ 100. Подзадача оценивается в 30 баллов.

  3. N ≤ 2000. Подзадача оценивается в 30 баллов.

  4. N ≤ 200 000. Подзадача оценивается в 40 баллов.

Примеры
Входные данные
2
zabacabab
Выходные данные
5
Входные данные
2
abc
Выходные данные
0
Страница: << 39 40 41 42 43 44 45 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест