Темы --> Информатика --> Алгоритмы
    Задачи на моделирование(78 задач)
    Арифметические алгоритмы(240 задач)
    Алгоритмы поиска(155 задач)
    Алгоритмы сортировки(194 задач)
    Динамическое программирование(355 задач)
    Алгоритмы на графах(319 задач)
    Перебор(154 задач)
    Игры и выигрышные стратегии(33 задач)
    Вычислительная геометрия(216 задач)
    Эвристические методы(30 задач)
    Алгоритмы на строках(45 задач)
    Пересечение множеств(10 задач)
    Жадный алгоритм(71 задач)
    Теория расписаний(5 задач)
    Обработка текста(31 задач)
    Дата и время(14 задач)
---> 151 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
#722
Пересадки
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На Новом проспекте для разгрузки было решено пустить два новых автобусных маршрута на разных участках проспекта.  Известны конечные остановки каждого из автобусов. Определите количество остановок, на  которых можно пересесть с одного автобуса на другой.

Входные данные

Вводятся четыре числа, не превосходящие 100, задающие номера конечных остановок. Сначала для первого, потом второго автобуса (см. примеры и рисунок).

Выходные данные

Ваша программа должна выводить одно число – искомое количество остановок.

 Задача В, рис. 2

Пояснения

Первый пример (см. рисунок): первый автобус ходит с 3-й остановки по 6-ю и обратно, а второй с 2-й по 4-ю и обратно. Пересесть с одного автобуса на другой можно на 3-й и 4-й остановках. Их две.

Второй пример: автобусы не имеют общих остановок.

Примеры
Входные данные
3 6 4 2
Выходные данные
2
Входные данные
3 1 5 10
Выходные данные
0
#727
Квас
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные

Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные

Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Задача Е, рис. 4Примеры

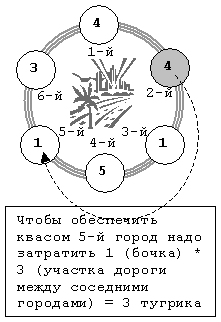
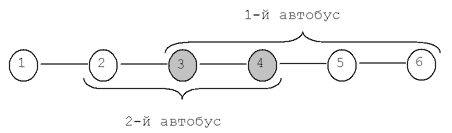
Пояснение для второго примера(см. рисунок):

На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Примеры
Входные данные
3 5 3 10
Выходные данные
3
Входные данные
6 4 4 1 5 1 3
Выходные данные
2
#1049
Горнолыжные соревнования
  
ограничение по времени на тест
0.5 second;
ограничение по памяти на тест
64 megabytes

Горнолыжник, готовясь к соревнованиям, нарисовал на бумаге схему горнолыжной трассы для выбора оптимального маршрута спуска. На схеме расположенные на трассе ворота представлены горизонтальными отрезками. Никакая пара ворот не имеет общих точек.

Маршрут должен представлять собой ломаную, начинающуюся в точке старта на вершине горы и заканчивающуюся в точке финиша у ее подножия. Маршрут выбирается таким образом, что y-координата каждой следующей вершины ломаной оказывается строго меньше y-координаты предыдущей вершины. Один из возможных маршрутов представлен на рисунке.

За каждые ворота, через которые не проходит маршрут, лыжнику начисляются штрафные очки. Общий штраф за спуск по маршруту вычисляется как сумма длины маршрута и штрафных очков за непройденные ворота.

Требуется написать программу, которая определяет, какой минимальный общий штраф горнолыжник может получить при прохождении трассы.

Входные данные

В первой строке входного файла задано число N - количество ворот на трассе (0 ≤ N ≤ 500), в следующих двух строках заданы Sx, Sy, Fx, Fy - координаты точек старта и финиша соответственно. В каждой из следующих N строк записаны четыре числа ai, bi, yi, ci - x-координаты левого и правого концов ворот, y-координата ворот и штраф за непрохождение данных ворот (ai < bi, Fy < yi < Sy, ci - целое число, 0 ≤ ci ≤ 10000). Все координаты - целые числа, не превосходящие по модулю 10000.

Выходные данные

В выходной файл выведите наименьший возможный общий штраф за прохождение трассы с точностью не менее 4 знаков после десятичной точки.

Система оценки

Потестовая.

Примеры
Входные данные
4
3 6
3 1
5 7 4 1
4 5 5 10
1 2 4 5
2 5 2 0
Выходные данные
7.8126
#1050
Фигурное программирование
  
#1051
Пекка развлекается
  
Страница: << 2 3 4 5 6 7 8 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест