Темы --> Информатика --> Структуры данных --> Линейные структуры
    Очередь(10 задач)
    Стек(35 задач)
    Дек(6 задач)
    Список(7 задач)
    Префиксные суммы(минимумы, ...)(2 задач)
---> 10 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 1 2 Отображать по:
#3866
Поврежденный XML
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Формат XML является распространенным способом обмена данными между различными программами. Недавно программист Иванов написал небольшую программу, которая сохраняет некоторую важную информацию в виде XML-строки.

XML-строка состоит из открывающих и закрывающих тегов.

Открывающий тег начинается с открывающей угловой скобки (<), за ней следует имя тега — непустая строка из строчных букв латинского алфавита, а затем закрывающая угловая скобка (>). Примеры открывающих тегов: <a>, <dog>.

Закрывающий тег начинается с открывающей угловой скобки, за ней следует прямой слеш (/), затем имя тега — непустая строка из строчных букв латинского алфавита, а затем закрывающая угловая скобка. Примеры закрывающихся тегов: </a>, </dog>.

XML-строка называется корректной, если она может быть получена по следующим правилам:

  • Пустая строка является корректной XML-строкой.
  • A и B — корректные XML-строки, то строка AB, получающаяся приписыванием строки B в конец строки A, также является корректной XML-строкой.
  • Если A — корректная XML-строка, то строка <X>A</X>, получающаяся приписыванием в начало A открывающегося тега, а в конец — закрывающегося с таким же именем, также является корректной XML-строкой. Здесь X — любая непустая строка из строчных букв латинского алфавита.

Например, представленные ниже строки:

<a></a>

<a><ab></ab><c></c></a>

<a></a><a></a><a></a>

являются корректными XML-строками, а такие строки как:

<a></b>

<a><b>

<a><b></a></b>

не являются корректными XML-строками.

Иванов отправил файл с сохраненной XML-строкой по электронной почте своему коллеге Петрову. Однако, к сожалению, файл повредился в процессе пересылки: ровно один символ в строке заменился на некоторый другой символ.

Требуется написать программу, которая по строке, которую получил Петров, восстановит исходную XML-строку, которую отправлял Иванов.

Входные данные

Входной файл содержит одну строку, которая заменой ровно одного символа может быть превращена в корректную XML-строку. Длина строки лежит в пределах от 7 до 1000, включительно. Строка содержит только строчные буквы латинского алфавита и символы «<» (ASCII код 60), «>»(ASCII код 62) и «/»(ASCII код 47).

Строка во входном файле заканчивается переводом строки.

Выходные данные

Выходной файл должен содержать корректную XML-строку, которая может быть получена из строки во входном файле заменой ровно одного символа на другой. Если вариантов ответа несколько, можно вывести любой.

Примеры входных и выходных файлов

input

output

<a></b>

<a></a>

<a><aa>

<a></a>

<a><>a>

<a></a>

<a/</a>

<a></a>


#111636
Древние династии
  

История Татаро-монгольского ханства богата на правителей. Каждый из N правителей принадлежал к одной из двух династий, причём власть часто переходила от одной династии к другой. Каждое восхождение правителя на престол отмечалось праздником, проводимым 26 марта. В летописях зафиксированы годы проведения этих праздников, причем известно, что правители первой династии устраивали для народа праздник кумыса, а второй — праздник мёда.

На конференции по истории Татаро-монгольского ханства каждый из S учёных предложил свою версию толкования летописи. А именно, i-й историк утверждал, что от каждого праздника кумыса до следующего праздника кумыса проходило не менее KLi лет, но не более KRi лет, в то время как от каждого праздника мёда до следующего праздника мёда проходило не менее MLi лет, но не более MRi лет.

Каждой предложенной версии может соответствовать несколько распределений правителей по династиям. Ученые договорились считать показателем сомнительности распределения число переходов власти к представителю той же самой династии.

Требуется написать программу, которая найдёт распределение, соответствующее хотя бы одной из версий и имеющее наименьший показатель сомнительности, а также версию, которой оно соответствует.

Входные данные

В первой строке входного файла записано число N (2 ≤ N ≤ 200 000) — количество праздников в летописи. Следующая строка содержит целые числа X1, X2, ..., XN (1 ≤ X1 ≤ X2 ≤ ... ≤ XN ≤ 109) — годы проведения праздников.

В третьей строке записано число учёных S (1 ≤ S ≤ 50). В каждой из последующих S строк записаны четыре натуральных числа KLi, KRi, MLi, MRi (1 ≤ KLi ≤ KRi ≤ 109), (1 ≤ MLi ≤ MRi ≤ 109).

Выходные данные

Первая строка выходного файла должна содержать числа P и Q, где P — номер учёного, версии которого соответствует распределение с наименьшим показателем сомнительности, а Q — показатель сомнительности этого распределения.

Вторая строка должна состоять из N цифр 1 и 2, записанных без пробелов, означающих приход к власти представителя первой или второй династии соответственно. Если существует несколько решений с наименьшим показателем сомнительности Q, выведите любое из них.

В случае, если ни в одной из версий учёных не существует способа распределения периодов правления между династиями так, чтобы не нарушались ограничения на промежутки времени между праздниками, выходной файл должен содержать единственное число 0.

Примечание

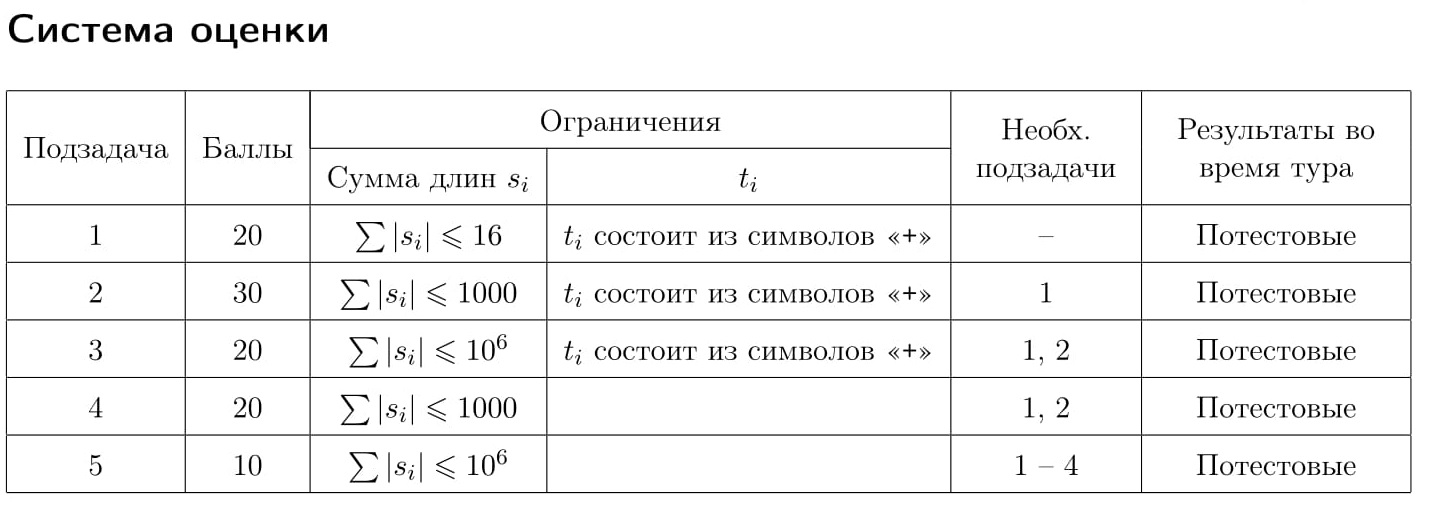
Данная задача содержит шесть подзадач. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

  1. Тесты из условия. Подзадача оценивается в 0 баллов.

  2. 2 ≤ N ≤ 15, 1 ≤ S ≤ 10. Подзадача оценивается в 20 баллов.

  3. 2 ≤ N ≤ 2000, 1 ≤ S ≤ 50, N × S ≤ 2000. Подзадача оценивается в 20 баллов.

  4. 2 ≤ N ≤ 10 000, 1 ≤ S ≤ 50, N × S ≤ 10 000. Подзадача оценивается в 20 баллов.

  5. 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50, N × S ≤ 200 000. Подзадача оценивается в 20 баллов.

  6. 2 ≤ N ≤ 200 000, 1 ≤ S ≤ 50. Подзадача оценивается в 20 баллов.

Примеры
Входные данные
3
1 2 3
1
1 1 1 1
Выходные данные
1 1
211
Входные данные
4
1 6 9 13
2
1 2 2 3
6 7 3 3
Выходные данные
0
Входные данные
5
3 6 8 9 10
2
2 3 1 1
1 4 1 10
Выходные данные
2 0
21212
#113544
Программирование квадрокоптеров
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Школьники готовятся к участию в соревновании по программированию квадрокоптеров. Квадрокоптер, который используется в соревновании, может выполнять две команды: подняться вверх на 1 метр и опуститься вниз на 1 метр. Команда подъёма обозначается символом «(», а команда спуска — символом «)».

Программа для квадрокоптера представляет собой последовательность команд. Программа считается корректной, если, начав её исполнение на уровне земли и выполнив последовательно все команды, квадрокоптер снова оказывается на уровне земли. При этом в процессе выполнения программы квадрокоптер не должен пытаться опуститься ниже уровня земли.

Например, следующие программы являются корректными: «()(())», «((()))». Программа«(((» не является корректной, поскольку квадрокоптер завершает ее выполнение на высоте 3 метра над уровнем земли, программа «())(» также не является корректной, поскольку при выполнении третьей команды квадрокоптер пытается опуститься ниже уровня земли.

Участник соревнования написал корректную программу для квадрокоптера, состоящую из n команд, пронумерованных от 1 до n. Он загрузил её в память квадрокоптера для демонстрации во время соревнования. К сожалению, после загрузки программы в память квадрокоптера участник случайно удалил её на своём компьютере, а квадрокоптер не позволяет выгрузить программу из своей памяти.

К счастью, квадрокоптер поддерживает специальный режим отладки программы. В этом режиме квадрокоптер с загруженной в него программой может отвечать на специальные запросы. Каждый запрос представляет собой два целых числа: l и r, 1 ≤ l ≤ r ≤ n. В ответ на запрос квадрокоптер сообщает, является ли фрагмент загруженной в него программы, состоящий из команд с l-й по r-ю включительно, корректной программой для квадрокоптера, либо нет. Участник хочет с помощью режима отладки восстановить загруженную в квадрокоптер программу.

Требуется написать программу-решение, которая взаимодействует с программой жюри, моделирующей режим отладки квадрокоптера, и в итоге восстанавливает загруженную в квадрокоптер программу.

Протокол взаимодействия

Это интерактивная задача.

Сначала на вход подаётся целое число n — количество команд в программе квадрокоптера (2 ≤ n ≤ 50 000).

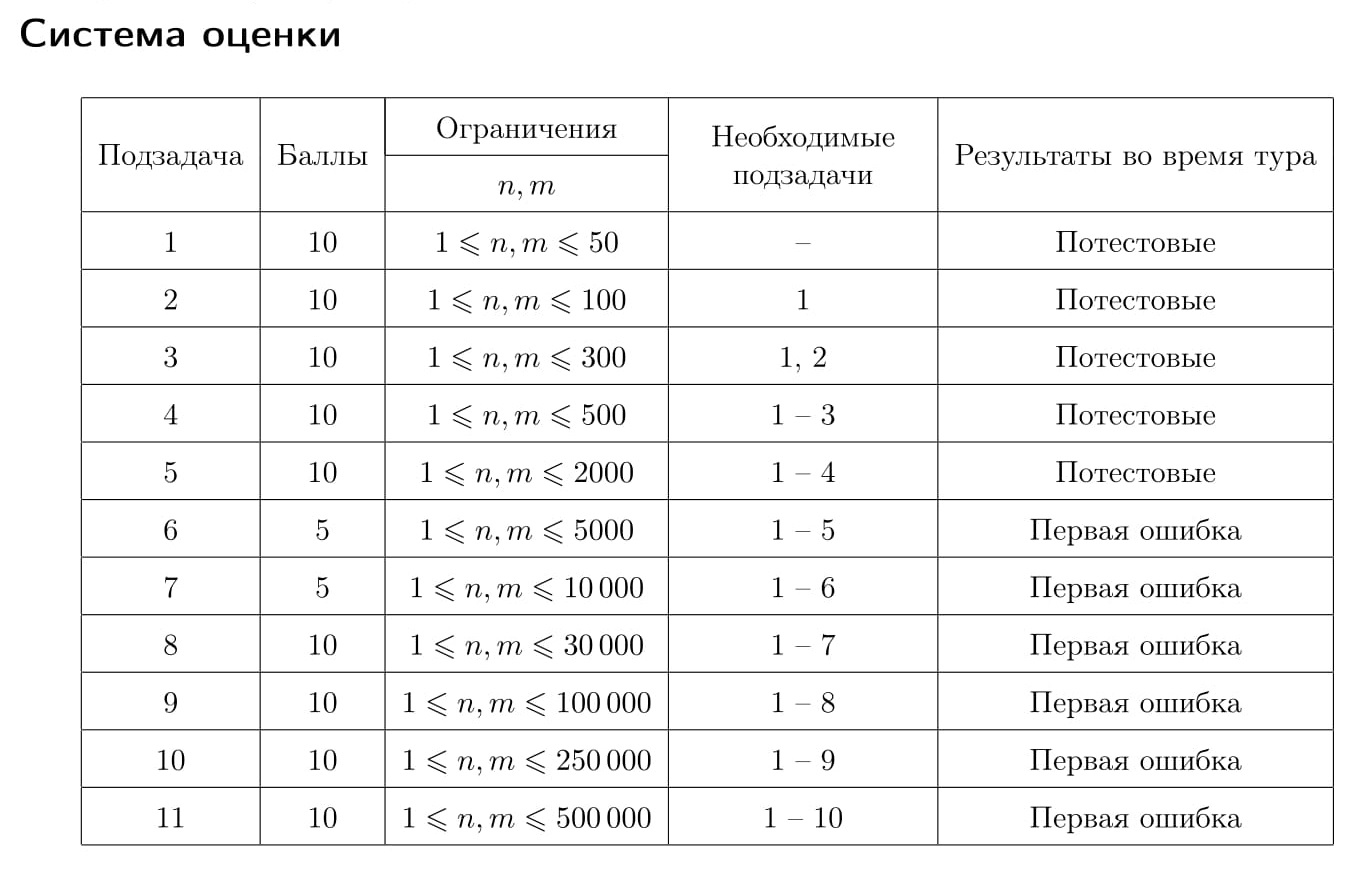
Для каждого теста жюри зафиксировано число k — максимальное количество запросов. Гарантируется, что k запросов достаточно, чтобы решить задачу. Это число не сообщается программе-решению. Ограничения k в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов к программе жюри, то на этом тесте она получает в качестве результата тестирования «Неверный ответ».

Чтобы сделать запрос, программа-решение должна вывести строку вида «? l r», где l и r — целые положительные числа, задающие фрагмент программы квадрокоптера (1 ≤ l ≤ r ≤ n).

В ответ на запрос программы-решения программа жюри подаёт ей на вход либо строку «Yes», либо строку «No», в зависимости от того, является ли запрошенный фрагмент программы квадрокоптера корректной программой.

Если программа-решение определила ответ на задачу, то она должна вывести строку «! c1c2... cn», где символ ci задаёт i-ю команду в программе квадрокоптера и равен либо «(», либо «)».

После этого программа-решение должна завершиться.

Гарантируется, что в каждом тесте программа в памяти квадрокоптера является фиксированной корректной программой, которая не меняется в зависимости от запросов, произведённых программой-решением.

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.

В первом примере n = 4. Единственная возможная корректная программа из двух команд это «()», поэтому из результатов третьего и четвёртого запросов можно сделать вывод, что программа в памяти квадрокоптера — «()()». Поэтому, в частности, ответ на второй запрос действительно «No», так как фрагмент программы «()(» не является корректной программой: если квадрокоптер исполнит именно эти три команды, он останется на уровне одного метра над землёй.

В втором примере n = 6, и произведённых запросов достаточно, чтобы однозначно определить, что программа в памяти квадрокоптера — «((()))».

В тестах из условия k = 150, то есть, разрешается произвести не более 150 запросов.

#113548
Накопитель
  
Темы: [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Исследуется новое цифровое устройство для хранения информации. Информация на устройстве хранится в виде последовательности ячеек, каждая из которых находится в одном из двух состояний, обозначаемых символами «+» и «-», и, таким образом, хранит один бит информации.

Назовём фрагментом группу соседних ячеек с одинаковым состоянием, слева от которой либо нет ячеек, либо находится ячейка в противоположном состоянии, и справа — либо нет ячеек, либо находится ячейка в противоположном состоянии.

Операция записи позволяет выбрать любую пару соседних фрагментов разной длины и изменить состояние всех ячеек более короткого фрагмента на противоположное, объединяя таким образом два или три соседних фрагмента в один.

Требуется написать программу, которая по заданной исходной и итоговой последовательностям состояний ячеек определяет, можно ли из исходной последовательности получить итоговую с помощью последовательных операций записи.

Входные данные

Первая строка входных данных содержит целое положительное число q — количество тестов.

Каждая из следующих q строк содержит si, ti — непустые последовательности символов «+» и «-» одинаковой длины, разделённые одним пробелом. Эта строка означает, что в тесте номер i из исходной последовательности состояний ячеек si требуется получить итоговую последовательность ti.

Выходные данные

Выходные данные должны содержать q строк, где i-я строка равна «Yes», если из исходной последовательности состояний ячеек si можно получить итоговую последовательность ti, или «No» в противном случае.

Примеры
Входные данные
3
++- +++
++-- ++++
++-+--+- ++++++++
Выходные данные
Yes
No
Yes
Входные данные
3
++-+-- ++----
++-+-- +++---
-++- -++-
Выходные данные
Yes
No
Yes
#113551
Траектория обучения
  
Темы: [Рекурсия] [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
512 megabytes

Победитель студенческой олимпиады получил предложения о стажировке от двух университетов. При подготовке планов обучения он узнал рейтинг качества преподавания каждой дисциплины в этих университетах.

Программа обучения первого университета состоит из последовательности перечисленных в хронологическом порядке n различных дисциплин a1, a2, ..., an, имеющих рейтинги x1, x2, ..., xn соответственно. Программа обучения второго университета состоит из последовательности перечисленных в хронологическом порядке m различных дисциплин b1, b2, ..., bm, имеющих рейтинги y1, y2, ..., ym соответственно.

Студент имеет возможность составить план обучения в первом университете таким образом, чтобы изучить дисциплины на позициях учебной программы с la по ra включительно (1 ≤ la ≤ ra ≤ n), либо отказаться от стажировки в первом университете. Аналогично он может составить план обучения во втором университете таким образом, чтобы изучить дисциплины на позициях учебной программы с lb по rb включительно (1 ≤ lb ≤ rb ≤ m), либо отказаться от стажировки во втором университете.

Изучать одну и ту же дисциплину дважды в разных университетах не имеет смысла, поэтому все дисциплины в двух выбранных планах обучения должны быть различны.

Требуется написать программу, которая определит планы обучения студента таким образом, чтобы получить наибольшую возможную сумму рейтингов изучаемых дисциплин.

Входные данные

Первая строка входных данных содержит целые числа n и m — количество дисциплин в программах обучения первого и второго университетов (1 ≤ n, m ≤ 500 000).

Вторая строка входных данных содержит n целых чисел ai — дисциплины, входящие в программу обучения первого университета, перечисленные в хронологическом порядке (1 ≤ ai ≤ n + m).

Третья строка входных данных содержит n целых чисел xi — рейтинги дисциплин, входящих в программу обучения первого университета, перечисленные том же порядке, что и дисциплины ai (1 ≤ xi ≤ 109).

Четвёртая строка входных данных содержит m целых чисел bi — дисциплины, входящие в программу обучения второго университета, перечисленные в хронологическом порядке (1 ≤ bi ≤ n + m).

Пятая строка входных данных содержит m целых чисел yi — рейтинги дисциплин, входящих в программу обучения второго университета, перечисленные том же порядке, что и дисциплины bi (1 ≤ yi ≤ 109).

Выходные данные

Первая строка выходных данных должна содержать целое число r — наибольшую возможную сумму рейтингов дисциплин.

Вторая строка выходных данных должна содержать целые числа la, ra — позиции в учебной программе первой и последней дисциплин, входящих в план обучения в первом университете, либо «0 0», если студент отказался от стажировки в первом университете.

Третья строка выходных данных должна содержать целые числа lb, rb — позиции в учебной программе первой и последней дисциплин, входящих в план обучения во втором университете, либо «0 0», если студент отказался от стажировки во втором университете.

Если возможных правильных ответов несколько, разрешается вывести любой из них.

Примечание

В первом тесте из условия приведённые планы обучения в университетах приводят к суммарному рейтингу дисциплин (7 + 4 + 10 + 1 + 5) + (5 + 3 + 4) = 27 + 12 = 39. Если бы студент выбрал только вторую и третью дисциплины в первом университете и весь курс обучения во втором университете, суммарный рейтинг дисциплин был бы (7 + 4) + (3 + 5 + 3 + 4 + 12) = 11 + 27 = 38.

Во втором тесте из условия первая и третья дисциплины во втором университете имеют настолько высокий рейтинг по сравнению с соответствующими дисциплинами первого университета, что наиболее выгодный вариант — пройти целиком стажировку во втором университете и отказаться от стажировки в первом университете.

Примеры
Входные данные
7 5
3 1 4 8 6 9 2
2 7 4 10 1 5 3
9 2 11 3 8
3 5 3 4 12
Выходные данные
39
2 6
2 4
Входные данные
2 3
1 2
1 4
2 3 1
17 2 15
Выходные данные
34
0 0
1 3
Входные данные
3 3
4 2 1
10 1 2
5 4 2
1 2 9
Выходные данные
19
1 1
3 3
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест