Перебор с отсечением(22 задач)
Простые задачи на перебор(43 задач)
Гамильтонов цикл(2 задач)
Окружная олимпиада(18 задач)
Региональный этап(109 задач)
Заключительный этап(97 задач)
Как много открытий можно сделать, исследуя числа и составляющие их цифры!
Петя очень любит арифметику, и кроме домашних заданий он постоянно придумывает дополнительные задачи. Однажды он стал прибавлять к натуральным числам сумму составляющих их цифр. Петя обнаружил, что некоторые числа, например 20, не могут быть получены из других чисел в результате такого действия. Эти числа ему не понравились, и он назвал их некрасивыми.
Позже, когда Петя начал изучать информатику, те же исследования он стал проводить с натуральными числами в двоичной системе счисления. Например, двоичное число 11102 (в десятичной системе — 14) можно получить из числа 11002 (в десятичной системе — 12), прибавив к последнему сумму его цифр:
11002 + 102 = 11102.
Петя решил исследовать множество двоичных некрасивых чисел. Первые пять некрасивых чисел он нашел без труда: 1 = 12, 4 = 1002, 6 = 1102, 13 = 11012, 15 = 11112. Продолжить работу он собирается с помощью компьютера.
Требуется написать программу, которая определяет количество двоичных некрасивых чисел, не превосходящих заданного числа n.
В первой строке входного файла содержится число n, записанное в десятичной системе счисления (1 ≤ n ≤ 1018).
В единственной строке выходного файла должно содержаться единственное число — количество двоичных некрасивых чисел, не превосходящих n.
Примечание
Решения, корректно работающие при n ≤ 106, будут оцениваться из 40 баллов.
17
5
18
6
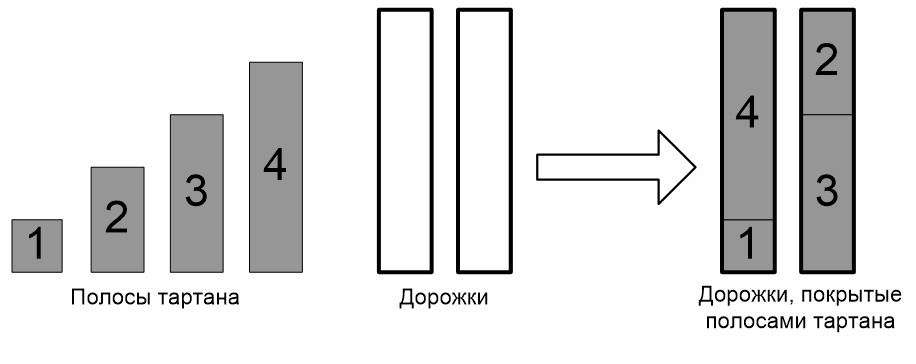
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
К 2110 году город Флэтбург, являясь одним из крупнейших городов мира, не имеет обходной автомагистрали, что является существенным препятствием для его развития как крупнейшего транспортного центра мирового значения. В связи с этим ещё в 2065 году при разработке Генерального плана развития Флэтбурга была определена необходимость строительства кольцевой автомобильной дороги.
В Генеральном плане также были обозначены требования к этой дороге. Она должна соответствовать статусу кольцевой — иметь форму окружности. Кроме этого, четыре крупные достопримечательности Флэтбурга должны быть в одинаковой транспортной доступности от дороги. Это предполагается обеспечить тем, что они будут находиться на равном расстоянии от неё. Расстоянием от точки расположения достопримечательности до дороги называется наименьшее из расстояний от этой точки до некоторой точки, принадлежащей окружности автодороги.
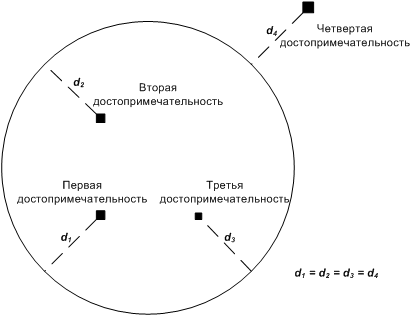
Требуется написать программу, которая вычислит число возможных планов постройки кольцевой автомобильной дороги с соблюдением указанных требований и найдёт такой план, для которого длина дороги будет минимальной. Гарантируется, что хотя бы один план постройки существует.
Входной файл содержит четыре строки. Каждая из них содержит по два целых числа: \(x_i\) и \(y_i\) — координаты места расположения достопримечательности. Первая строка описывает первую достопримечательность, вторая — вторую, третья — третью, четвёртая — четвёртую. Никакие две достопримечательности не находятся в одной точке.
Все числа во входном файле не превосходят 100 по абсолютной величине.
В первой строке выходного файла требуется вывести число возможных планов постройки кольцевой автомобильной дороги. Если таких планов бесконечно много, необходимо вывести в первой строке выходного файла слово Infinity.
На второй строке требуется вывести координаты центра дороги минимальной длины и её радиус. Если существует несколько разных способов построения дороги минимальной длины, необходимо вывести координаты центра и радиус любой из них. Координаты центра и радиус должны быть выведены с точностью не хуже \(10^{-5}\) и не должны превышать \(10^9\). Гарантируется, что существует хотя бы один план с такими параметрами.
0 0 0 1 1 0 2 2
7 1.5 0.5 1.14412281
0 0 0 1 1 0 1 1
Infinity 0.5 0.5 0.0
В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.
Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.
К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.
Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.
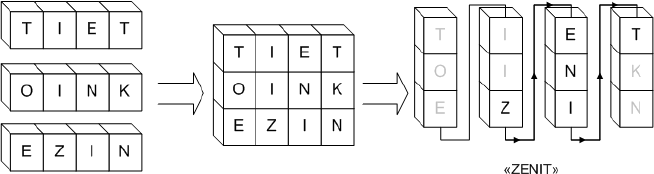
После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».
Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.
Первая строка входного файла содержит два натуральных числа \(N\) и \(L\) — число различных типов блоков на складе и длина каждого блока соответственно (\(1\le N\le100\), \(1\le L\le100\)). Последующие \(N\) строк содержат по одной записи длиной \(L\), состоящей из строчных латинских букв — надписи на блоках соответствующего типа. Надписи на блоках разных типов не совпадают.
Последняя строка входного файла содержит новую рекламную надпись \(s\) — строку, состоящую только из строчных латинских букв (\(1\le|s|\le200\)). Можно считать, что на складе находится неограниченное число блоков каждого типа.
В первой строке выходного файла необходимо вывести натуральное число \(K\) — минимальное количество блоков, которое нужно использовать для составления новой рекламы. Следующая строка должна содержать \(K\) чисел — номера типов блоков, которые нужно для этого использовать, перечисляя их сверху вниз. Типы блоков нумеруются с единицы в порядке их задания во входном файле.
Если ответов несколько, выведите любой из них. Если решения не существует, выведите в выходной файл число \(-1\).
3 4 tiet oink ezin zenit
3 1 2 3
2 11 sillysample happysample sam
1 2
2 3 baa aab bb
2 2 2
2 3 aaa bbb cc
-1
Cреди всех прямоугольных параллелепипедов с натуральными длинами сторон и площадью поверхности не более \(n\) найти тот, объём которого максимален.
Начинающий программист Поликарп очень любит дарить подарки, особенно в коробках. Он давно заметил, что если коробка красиво оформлена, то радость от подарка возрастает многократно. Любой обёрточной бумаге он предпочитает клетчатую. В самом деле, после распаковки подарка на ней можно играть в крестики-нолики, морской бой, точки, а также решать задачи и писать программы.
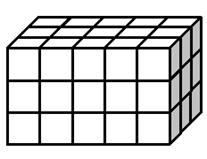
Поликарп очень аккуратен. Он упаковывает подарок в коробку, имеющую форму прямоугольного параллелепипеда, и оклеивает всю её поверхность клетчатой бумагой. При этом каждая грань коробки представляет собой прямоугольник, состоящий из целых клеток. На рисунке изображён пример такой упаковки подарка.
В настоящий момент Поликарп собирается поздравить свою подругу, недавно вернувшуюся с очередной олимпиады. Он хочет подарить ей подарок в большой и красивой коробке.
У Поликарпа в наличии есть лист клетчатой бумаги, состоящий из \(n\) клеток. Каким будет максимальный объём коробки, которую можно оклеить с использованием этого листа бумаги описанным выше способом? Поликарп может разрезать лист клетчатой бумаги по границам клеток произвольным образом и оклеивать коробку получившимися фигурами, поэтому форма листа не важна, а имеет значение только количество клеток на нём. Поликарп может использовать для оклеивания коробки не все клетки.
Напишите программу, которая по заданному количеству клеток \(n\) находит размеры коробки максимального возможного объема.
Входной файл содержит одно целое число \(n\) (\(6\le n\le10^{13}\)) — количество клеток на листе клетчатой бумаги.
Выведите в первую строку выходного файла максимальный объём коробки, которую может подарить Поликарп. Объём следует выводить в «кубических клетках», то есть единицей измерения является куб со стороной, равной длине стороны клетки.
Во вторую строку выведите ширину, длину и высоту искомой коробки. Единица измерения — размер клетки. Числа разделяйте пробелами. Если решений несколько, то выведите любое из них.
Система оценивания
Решения, корректно работающие при \(n\le5\,000\), будут оцениваться из 30 баллов, а решения, корректно работающие при \(n\le10^8\), будут оцениваться из 70 баллов.
6
1 1 1 1
24
8 2 2 2