#1929

Новое слово в рекламе

Темы: [Строки] [Алгоритмы на строках] [Простые задачи на перебор]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2010, 2 день, Задача D ]

В наши дни предоставление поверхностей заборов и стен промышленных зданий рекламодателям — уже не оригинальный способ получить дополнительный заработок, а нечто само собой разумеющееся.

Небольшая компания «Домострой» также решила выйти на этот рынок и стала предлагать место для рекламы на своих блоках заборов. Блок представляет собой параллелепипед размером \(1\times1\times L\), на одной из сторон которого есть место для рекламы — пространство размера \(1\times L\), в которое можно вписать ровно \(L\) букв латинского алфавита.

К сожалению, иногда сделки у компании срывались, и заранее подготовленные блоки с рекламой отправлялись на склад. Со временем там скопилось приличное количество блоков различных типов (блоки разных типов отличаются друг от друга только надписью), поэтому было решено использовать их вторично.

Была предложена следующая идея: если поставить несколько блоков друг на друга и закрасить ненужные буквы, то, читая сверху вниз и слева направо, можно будет прочитать какой-нибудь другой текст, как показано на рисунке.

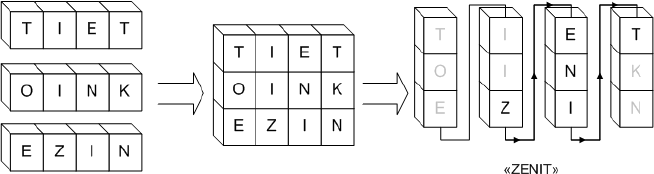
Таким образом, можно получить рекламную надпись для нового клиента. При этом из эстетических соображений при прочтении конечной надписи разрывы в виде закрашенных букв недопустимы.

После того, как некоторое число \(K\) блоков, каждый из которых имеет длину \(L\), поставили друг на друга, получилась прямоугольная таблица размером \(K\times L\), в каждой клетке которой находится буква латинского алфавита. Каждый рекламный блок соответствует строке этой таблицы. Теперь содержимое этой таблицы выписывается по столбцам, начиная с самого левого. При этом в каждом столбце буквы выписываются сверху вниз. В случае, изображённом на рисунке, в результате этого процесса получилась бы строка «TOEIIZENITKN». Необходимо, чтобы рекламная надпись, требуемая заказчику, входила в получившуюся строку как подстрока «TOEIIZENITKN».

Требуется написать программу, которая будет определять, какое минимальное количество блоков надо использовать, чтобы получить рекламную надпись, необходимую заказчику. При этом можно считать, что на складе блоков каждого типа неограниченно много.

Входные данные

Первая строка входного файла содержит два натуральных числа \(N\) и \(L\) — число различных типов блоков на складе и длина каждого блока соответственно (\(1\le N\le100\), \(1\le L\le100\)). Последующие \(N\) строк содержат по одной записи длиной \(L\), состоящей из строчных латинских букв — надписи на блоках соответствующего типа. Надписи на блоках разных типов не совпадают.

Последняя строка входного файла содержит новую рекламную надпись \(s\) — строку, состоящую только из строчных латинских букв (\(1\le|s|\le200\)). Можно считать, что на складе находится неограниченное число блоков каждого типа.

Выходные данные

В первой строке выходного файла необходимо вывести натуральное число \(K\) — минимальное количество блоков, которое нужно использовать для составления новой рекламы. Следующая строка должна содержать \(K\) чисел — номера типов блоков, которые нужно для этого использовать, перечисляя их сверху вниз. Типы блоков нумеруются с единицы в порядке их задания во входном файле.

Если ответов несколько, выведите любой из них. Если решения не существует, выведите в выходной файл число \(-1\).

Примеры

Входные данные

3 4
tiet
oink
ezin
zenit

Выходные данные

3
1 2 3

Входные данные

2 11
sillysample
happysample
sam

Выходные данные

1
2

Входные данные

2 3
baa
aab
bb

Выходные данные

2
2 2

Входные данные

2 3
aaa
bbb
cc

Выходные данные

-1

#3139

Лицензионные ключи

Темы: [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, Московская областная олимпиада, 2008, Задача A ]

Компания Macrohard выпустила в свет новую версию операционной системы «Frames» («Рамки») и теперь стремится внедрить ее на рынок информационных технологий. Каждая фирма, заказывающая новую версию «Рамок», получает лицензионные ключи от компании Macrohard по следующим правилам:

каждой копии присваивается уникальный 25-разрядный ключ, состоящий из цифр и заглавных букв латинского алфавита. Код разбивается на группы по 5 символов, которые разделяются между собой знаком «-»
по каждому ключу можно вычислить его контрольную сумму по следующему правилу: необходимо сложить веса значащих символов и взять остаток от деления этой суммы на некое число P, где вес символа есть
- значение цифры, если символ является цифрой (то есть вес цифры 5 равен пяти)
- порядковый номер буквы в латинском алфавите плюс 9 (то есть вес буквы F равен 15)

Например, для кода 12345-12345-12345-12345-12345 при P = 11 контрольная сумма равна (1+2+3+4+5)*5 mod 11 = 9

контрольная сумма является идентификатором фирмы, которая покупает операционные системы, следовательно, оно должно быть различным для разных юридических лиц.

Операционной системой заинтересовался один влиятельный человек, пожелавший установить ее на свой персональный компьютер. Вам, как работнику отдела лицензирования Macrohard, поручено сгенерировать новый ключ, который не только не повторяется с выданными ранее ключами, но и обладает новой (не используемой ранее) контрольной суммой. Требуется написать программу, которая решает эту задачу.

Входные данные

В первой строке входного файла содержится два натуральных числа N и P (1 ≤ N ≤ 30000, 1 ≤ P ≤ 1000), где N – число уже использованных ключей, P – число, используемое для подсчета контрольной суммы. В следующих N строках следуют ключи, которые задаются в виде
XXXXX-XXXXX-XXXXX-XXXXX-XXXXX, где X – значащий символ (цифра или буква латинского алфавита).

Выходные данные

В выходной файл требуется вывести новый уникальный ключ в соответствии с указанным форматом, обладающий уникальной контрольной суммой. В случае, если такой ключ сгенерировать невозможно, выведите слово «Impossible».

Ввод	Вывод
3 5 23545-14978-59345-87926-52496 67955-58818-19438-55659-02068 99185-57241-15114-39158-36125	01389-28172-62843-79648-28129
5 3 BGPOV-D618J-FTN7L-4QWZJ-E6P8S 7K3J3-I8076-58COS-0066F-9UAT4 7S17C-YI099-1UC85-5S9PB-772LT TN2I4-TC1Z6-1OLI6-LT43G-9JMD3 73OQ3-A9NBJ-N7UT7-AI349-XYJDT	1APMP-RSO53-G743I-F5TK6-R6487
5 4 7911L-5D41U-0N09C-34T16-5D0KI FRLAX-RE1Y1-WFVU0-88R56-C5D4V RUG51-IR00T-8L812-R6056-7OM59 804F2-L7292-I12PX-14NDO-02LEW J3QQ4-H7H2V-2HCH4-M3HK8-6M8VW	Impossible

#3871

«Abracadabra»

Темы: [Хеш] [Бор] [Бинарный поиск в массиве] [Строки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2012, 2 день, Задача D ]

Строка s называется супрефиксом для строки t, если t начинается с s и заканчивается на s. Например, «abra» является супрефиксом для строки «abracadabra». В частности, сама строка t является своим супрефиксом. Супрефиксы играют важную роль в различных алгоритмах на строках.

В этой задаче требуется решить обратную задачу о поиске супрефикса, которая заключается в следующем. Задан словарь, содержащий n слов t₁, t₂, …, t_n и набор из m строк-образцов s₁, s₂, …, s_m. Необходимо для каждой строки-образца из заданного набора найти количество слов в словаре, для которых эта строка-образец является супрефиксом.

Требуется написать программу, которая по заданному числу n, n словам словаря t₁, t₂, …, t_n, заданному числу m и m строкам-образцам s₁, s₂, …, s_m вычислит для каждой строки-образца количество слов из словаря, для которых эта строка-образец является супрефиксом.

Входные данные

Первая строка входного файла содержит целое число n (1 ≤ n ≤ 200 000).

Последующие n строк содержат слова t₁, t₂, …, t_n_, по одному слову в каждой строке. Каждое слово состоит из строчных букв латинского алфавита. Длина каждого слова не превышает 50. Суммарная длина всех слов не превышает 10⁶. Словарь не содержит пустых слов.

Затем следует строка, содержащая целое число m (1 ≤ m ≤ 200 000).

Последующие m строк содержат строки-образцы s₁, s₂, …, s_m, по одной на каждой строке. Каждая строка-образец состоит из строчных букв латинского алфавита: Длина каждой строки-образца не превышает 50. Суммарная длина всех строк-образцов не превышает 10⁶. Никакая строка-образец не является пустой строкой.

Выходные данные

Выходной файл должен содержать m чисел, по одному на строке.

Для каждой строки-образца в порядке, в котором они заданы во входном файле, следует вывести количество слов словаря, для которых она является супрефиксом.

Система оценки

Решения, работающие при \(n\), \(m\) не превосходящими 100 оцениваются из 30 баллов.

Примеры

Входные данные

4
abacaba
abracadabra
aa
abra
3
a
abra
abac

Выходные данные

4
2
0

#111634

Робот

Темы: [Строки] ["Два указателя"]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2013, 1 день, Задача B ]

Студенты одного из вузов спроектировали робота для частичной автоматизации процесса сборки авиационного двигателя.

В процессе сборки двигателя могут встречаться операции 26 типов, которые обозначаются строчными буквами латинского алфавита. Процесс сборки состоит из N операций.

Предполагается использовать робота один раз для выполнения части подряд идущих операций из процесса сборки.

Память робота состоит из K ячеек, каждая из которых содержит одну операцию. Операции выполняются последовательно, начиная с первой, в том порядке, в котором они расположены в памяти. Выполнив последнюю из них, робот продолжает работу с первой. Робота можно остановить после любой операции. Использование робота экономически целесообразно, если он выполнит хотя бы K + 1 операцию.

Требуется написать программу, которая по заданному процессу сборки определит количество экономически целесообразных способов использования робота.

Входные данные

В первой строке входного файла записано число K > 0 "— количество операций, которые можно записать в память робота.

Вторая строка состоит из N > K строчных латинских букв, обозначающих операции "— процесс сборки двигателя. Операции одного и того же типа обозначаются одной и той же буквой.

Выходные данные

Выходной файл должен содержать единственное целое число "— количество экономически целесообразных способов использования робота.

Примечание

Данная задача содержит четыре подзадачи. Для оценки каждой подзадачи используется своя группа тестов. Баллы за подзадачу начисляются только в том случае, если все тесты из этой группы пройдены.

Тесты из условия. Подзадача оценивается в 0 баллов.

N ≤ 100. Подзадача оценивается в 30 баллов.

N ≤ 2000. Подзадача оценивается в 30 баллов.

N ≤ 200 000. Подзадача оценивается в 40 баллов.

Примеры

Входные данные

2
zabacabab

Выходные данные

Входные данные

2
abc

Выходные данные

#111857

Телефонные номера

Темы: [Строки] [Обработка текста]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2012, Задача D ]

Телефонные номера в адресной книге мобильного телефона имеют один из следующих форматов:

+7<код><номер>

8<код><номер>

<номер>

где <номер> — это семь цифр, а <код> — это три цифры или три цифры в круглых скобках. Если код не указан, то считается, что он равен 495. Кроме того, в записи телефонного номера может стоять знак “-” между любыми двумя цифрами (см. пример).

На данный момент в адресной книге телефона Васи записано всего три телефонных номера, и он хочет записать туда еще один. Но он не может понять, не записан ли уже такой номер в телефонной книге. Помогите ему!

Два телефонных номера совпадают, если у них равны коды и равны номера. Например, +7(916)0123456 и 89160123456 — это один и тот же номер.

Входные данные

В первой строке входных данных записан номер телефона, который Вася хочет добавить в адресную книгу своего телефона. В следующих трех строках записаны три номера телефонов, которые уже находятся в адресной книге телефона Васи.

Гарантируется, что каждая из записей соответствует одному из трех приведенных в условии форматов.

Выходные данные

Для каждого телефонного номера в адресной книге выведите YES (заглавными буквами), если он совпадает с тем телефонным номером, который Вася хочет добавить в адресную книгу или NO (заглавными буквами) в противном случае.

Примеры

Входные данные

8(495)430-23-97
+7-4-9-5-43-023-97
4-3-0-2-3-9-7
8-495-430

Выходные данные

YES
YES
NO