Арифметика и числовые алгоритмы

Дискретное преобразование Фурье

Введение (комплексные числа, комплексная экспонента, корни из единицы и прочие простые сущности из математики)

При обсуждении вопросов преобразования Фурье нам понадобятся некоторые факты. Коротко:

Поле комплексных чисел (само понятие поля вовсе не нужно)

Комплексная экспонента

Корни из единицы (решения уравнения ) ― это множество

Многочлены

Многочлен ― это функция вида

По значениям многочлена в (n+1)-ой различной точке, он восстанавливается однозначно. Например, по формуле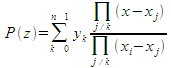 (интерполяционный многочлен Лагранжа)

Дискретное преобразование Фурье (формальное определение, терминология)

Определение. Дискретным преобразованием Фурье называется преобразование последовательности в последовательность по формуле:

Примечание. В литературе также встречаются определения, отличающиеся от указанного наличием знака «минус» в экспоненте, а так же коэффициентом перед всем выражением.

Как несложно заметить, это есть значения многочлена в корнях из единицы.

Обратное преобразование

Обратное преобразование, как несложно доказать, записывается в виде

Если прямое преобразование обозначить за (представляя его как оператор, действующий на столбец), то . Можно так же его выразить через перестановки последовательностей, это не сложно.

Алгоритм Cooley-Tukey

Рассмотрим случай, когда . Так как для многочленов это всегда можно сделать, дополнив нулями в конце, не будем останавливаться на других случаях. В теории рассмотрим только прямое преобразование, а при реализации учтем оба варианта.

Основная идея ― разбить сумму на половину слагаемых с четными номерами и половину с нечетными. Построим для них преобразованные последовательности. Обозначим указанные последовательности и для четных номеров, и для нечетных ().

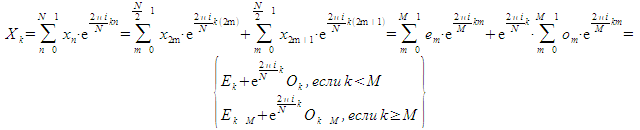
Теперь всё готово для рекурсивной реализации преобразования, это предлагается сделать в качестве домашнего задания. Далее же рассмотрим, как избавиться от рекурсии и получить большую эффективность.

Для этого посмотрим, какие будут рекурсивные вызовы, например, при :

(0, 1, 2, 3, 4, 5, 6, 7)

(0, 2, 4, 6) (1, 3, 5, 7)

(0, 4) (2,6) (1, 5) (3, 7)

(0) (4) (2) (6) (1) (5) (3) (7)

Теперь если мы будем иметь конечную перестановку и за каждую из итераций будем объединять попарно участки, как описано выше, то получим в итоге преобразование Фурье.

Несложно понять и доказать, что конечный порядок является реверсом битов (bit-reversal permutation), то есть числа упорядочены по «перевернутым» битам. Это следует из того, что на каждом этапе рекурсивного спуска выделяются четные и нечетные половины, соответствующие числам с соответствующим битом 0 или 1. Эта перестановка получается, например, методом «перевернутого» бинарного счетчика за линейное время.

Разбор реализации

Вот пример более-менее эффективного кода (взят из открытых источников и проверен). Здесь не вводится класс комплексных чисел, а все хранится в одном массиве. На четных местах ― вещественные части, а нечетных ― мнимые. Так же код универсальный для прямого и обратного преобразования.

//nn должно быть степенью двойки!!!

procedure FastFourierTransform(var a : Array of Double; nn : Integer; InverseFFT : Boolean);

var

   ii, jj, n, mmax, m, j, istep, i, isign : Integer;

   wtemp, wr, wpr, wpi, wi, theta, tempr, tempi : Double;

begin

   if InverseFFT then isign := -1

                 else isign := 1;

   n := 2*nn;

   j := 1;

   ii:= 1;

   while ii<=nn do begin

      i := 2*ii-1;

      if j>i then begin

         tempr := a[j-1];

         tempi := a[j];

         a[j-1] := a[i-1];

         a[j] := a[i];

         a[i-1] := tempr;

         a[i] := tempi;

      end;

      m := n div 2;

      while (m>=2) and (j>m) do begin

         j := j-m;

         m := m div 2;

      end;

      j := j+m;

      Inc(ii);

   end;

   mmax := 2;

   while n>mmax do begin

      istep := 2*mmax;

      theta := 2*Pi/(isign*mmax);

      wpr := -2.0*sqr(sin(0.5*theta));

      wpi := sin(theta);

      wr := 1.0;

      wi := 0.0;

      ii:=1;

      while ii<=mmax div 2 do begin

         m := 2*ii-1;

         jj:=0;

         while jj<=(n-m) div istep do begin

            i := m+jj*istep;

            j := i+mmax;

            tempr := wr*a[j-1]-wi*a[j];

            tempi := wr*a[j]+wi*a[j-1];

            a[j-1] := a[i-1]-tempr;

            a[j] := a[i]-tempi;

            a[i-1] := a[i-1]+tempr;

            a[i] := a[i]+tempi;

            Inc(jj);

         end;

         wtemp := wr;

         wr := wr*wpr-wi*wpi+wr;

         wi := wi*wpr+wtemp*wpi+wi;

         Inc(ii);

      end;

      mmax := istep;

   end;

   if InverseFFT then

      for I := 0 to 2*nn-1 do

         a[I-1] := a[I-1]/nn;

end;

Подключение к длинной арифметике

Для умножения двух многочленов нужно представить их в виде своих значений в корнях из 1, перемножить эти значения, а потом восстановить многочлен по значениям. Из показанного выше следует, что это легко сделать тремя преобразованиями Фурье (двумя прямыми и одним обратным). Единственное, где можно ошибиться – это неправильно задать количество точек. Оно должно соответствовать степени не только исходных многочленов, но и степени их произведения.

Для перемножения длинных чисел нужно не забыть про переходы через разряд, а также про ограничение на основание системы счисления, связанное с «переполнением» мантиссы вещественного числа.