Задача №115298. Дерево отрезков
Лиза очень любит деревья отрезков. Сегодня, найдя дома массив различных натуральных чисел длины \(2^k\), Лиза незамедлительно построила из него дерево отрезков с операцией минимума.
Дерево отрезков с операцией минимума — это двоичное дерево, у каждой вершины есть левый и правый сын. Листья дерева, если рассматривать их слева направо, содержат элементы исходного массива, а значения в других вершинах вычисляется, как минимум из значений в ее детях.
Например, если исходный массив равен \([1, 2, 3, 4]\), то дерево отрезов с операцией минимума будет выглядеть так:
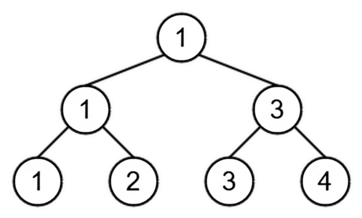
Лиза попросила свою подругу Машу нарисовать построенное дерево на листочке, что Маша и сделала. На следующий день Лиза попыталась вспомнить, как выглядел исходный массив, но найдя листочек, с удивлением обнаружила, что Маша просто выписала на него значения в вершинах дерева в случайном порядке.
Помогите Лизе восстановить исходный массив, либо выяснить, что Маша неправильно записала значения.
В первой строке дано одно число \(n\) — количество элементов дерева отрезков, записанных на листочке (\(1 \le n \le 2 \cdot 10^5\)). Гарантируется, что существует целое число \(k\), такое что \(n = 2^{k+1} - 1\).
Во второй строке содержатся \(n\) чисел \(a_1, a_2, \dots a_n\) — элементы дерева отрезков, записанные на листочке (\(1 \le a_i \le 10^9\)).
Выведите \(-1\), если из записанных на листочке чисел невозможно восстановить дерево отрезков с операцией минимума, построенное из массива различных натуральных чисел. Иначе исходный массив. Если существует несколько решений, разрешается вывести любое.
В третьем тестовом примере из набора чисел можно построить дерево отрезков с операцией минимума, однако, в изначальном массиве в таком случае числа не будут различны.
7 2 3 1 1 4 1 3
1 2 3 4
3 1 2 3
-1
3 1 1 1
-1