Задача №1707. Рисунки и пустоты
Представьте себе бесконечную клетчатую бумагу. Изначально все клетки белые, но некоторые из них можно закрасить черным.
Назовем две клетки 8-связными, если у них есть общая сторона или точка. 8-путем назовем последовательность клеток от A до B, так что все клетки в последовательности черные, и две соседние клетки в последовательности являются 8-связными. Набор черных клеток назовем рисунком, если существует 8-путь из каждой клетки набора в любую другую клетку этого набора.
Назовем две клетки 4-связными, если у них есть общая сторона. 4-путем назовем последовательность клеток от A до B, так что все клетки в последовательности белые, и две соседние клетки в последовательности являются 4-связными. Конечный набор белых клеток назовем пустотой, если существует 4-путь из каждой клетки набора в любую другую клетку этого набора и к нему невозможно добавить ни одной белой клетки так, чтобы предыдущее условие не нарушилось.
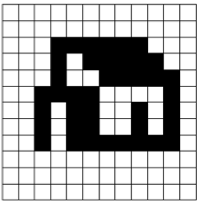
Будем говорить, что рисунок имеет высоту H и ширину W если он охватывается прямоугольником с высотой H и шириной W и не охватывается никаким прямоугольником меньшего размера. На иллюстрации показан рисунок с высотой 7 и шириной 9. По заданным числа H, W и N постройте рисунок высоты H, ширины W содержащий ровно N пустот.
Входной файл содержит несколько тестовых блоков. Первая строка содержит число T (1 ≤ T ≤ 100) – количество тестовых блоков.
Каждая из следующих T строк описывает один тестовый блок. Описание состоит из целых чисел H, W и N (1 ≤ H, W ≤ 20, 1 ≤ N ≤ 200).
Выходной файл должен содержать следующую информацию для каждого тестового блока:
Если рисунок можно построить, то выведите любую допустимую фигуру, удовлетворяющую условию задачи, состоящую из H строк по W символов в каждой. Выводите символ “.” для обозначения черной клетки и символ “#” для обозначения белой клетки.
Если рисунок построить нельзя, выведите одну строку, содержащую слово “Impossible”.
Вывод данных для разных тестовых блоков разделяйте одной пустой строкой.
3 7 9 2 20 20 22 5 5 10
#......## #.#.....# #.##..... ....####. .#..##.#. .#..##.#. .#....... .#####.######.#####. ..###...####...###.. ...#.....##.....#... .................... ....##..##..#...#... ...#.#.#..#.##.##... ...###.#....#.#.#... ...#.#.#..#.#...#... ...#.#..##..#...#... .................... .................... .###..##..###...##.. ..#..#..#.#..#.#..#. ..#..#....###..#.... ..#..#..#.#....#..#. .###..##..#.....##.. .................... ...#.....##.....#... ..###...####...###.. .#####.######.#####. Impossible